PDH锁频技术
PDH激光稳频技术
介绍
基于频率调制(FM)。PHD技术是提高激光频率稳定性的技术。激光频率由FP腔测得,测量结果反馈到激光器中抑制频率漂移。好处是系统不会被FP腔的响应时间限制,频率浮动比腔的响应速度快。
概念模型
很多现代激光器是可调谐的,自带能反馈电信号的输入接口调节输出频率。如果能精确测量激光频率,并反馈回调谐接口,借助控制系统,能保持频率不变。
FP腔原理
在光学中,法布里-佩罗干涉仪(英文:Fabry–Pérot interferometer)是一种由两块平行的玻璃板组成的多光束干涉仪,其中两块玻璃板相对的内表面都具有高反射率。法布里-佩罗干涉仪也经常称作法布里-佩罗谐振腔、F-P腔或法-珀腔(英語:F-P Cavity),并且当两块玻璃板间用固定长度的空心间隔物来间隔固定时,它也被称作法布里-佩罗标准具或直接简称为标准具(来自法语étalon, 意为“测量规范”或“标准”),但这些术语在使用时并不严格区分。这一干涉仪的特性为,当入射光的频率满足其共振条件时,其透射频谱会出现很高的峰值,对应着很高的透射率。法布里-佩罗干涉仪这一名称来自法国物理学家夏尔·法布里和阿尔弗雷德·佩罗(摘自wiki)。
当FP腔尺寸远大于入射波长,可用多光束干涉进行描述。
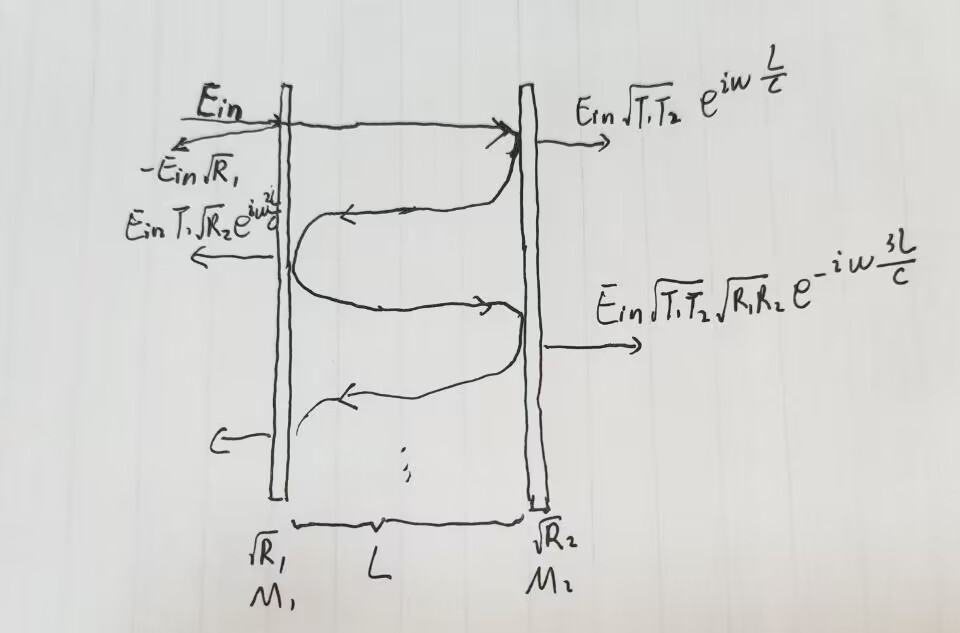
如图,入射光为\(E_{in}\),两镜透射系数和反射系数分别为\(T_1, ~ T_2\)和\(R_1, ~ R_2\)。两镜间隔为\(L\)。
不考虑吸收有\(T_1 + R_1=1; ~ T_2 + R_2 = 1\),入射光被\(M_1\)外侧反射为\(E_{ in }\sqrt{R_1}\)。在薄膜介质折射率\(n_1, n_2\)相等条件下,折射率有如下关系\(r = -r'\),相位反转180度。
反射光强
\[ \begin{aligned} E_{ref} &= -E_{in}\sqrt{R_1} + E_{in}T_1\sqrt{R_2}e^{iw\frac{2L}{C}} + E_{in}T_1\sqrt{R_2}\sqrt{R_1 R_2}e^{iw\frac{4L}{C}} + ... \\ &= -E_{in}\sqrt{R_1} + E_{in}T_1\sqrt{R_2}e^{iw\frac{2L}{C}} \left( 1 + \sqrt{R_1 R_2}e^{iw\frac{2L}{C}} + R_1 R_2e^{iw\frac{4L}{C}} + ... \right) \\ &= -E_{in}\sqrt{R_1} + E_{in}T_1\sqrt{R_2}e^{iw\frac{2L}{C}} \cdot \frac{1}{ 1 - \sqrt{R_1 R_2}e^{iw\frac{2L}{C}} } \end{aligned} \]
若两个镜子反射率相同,即\(R_1 = R_2 = r^2\),其中\(R\)为光强反射率,r为振幅反射率。则原式 \[ \begin{aligned} &= -E_{in}r + \frac{ E_{in}(1 - R_1 )r e^{iw\frac{2L}{C}} }{ 1 - r^2 e^{iw\frac{2L}{C}} }, ~~~~ \Delta\nu_{fsr} = \frac{C}{2L} \\ &= -E_{in}r + \frac{ E_{in}(1 - r^2 )r e^{iw\frac{1}{\Delta\nu_{fsr}}} }{ 1 - r^2 e^{iw\frac{1}{\Delta\nu_{fsr}}} } \end{aligned} \]
故电场反射耦合系数 \[ \begin{aligned} F(w) &= \frac{ E_{ref} }{ E_{in} } = -r + \frac{ (1-r^2)r e^{iw \frac{1}{\Delta\nu_{fsr}}} }{ 1 - r^2e^{iw\frac{1}{\Delta\nu_{fsr}} }} \\ &= \frac{ E_{ref} }{ E_{in} } = \frac{ r (e^{iw \frac{1}{\Delta\nu_{fsr}}} - 1) }{ 1 - r^2e^{iw\frac{1}{\Delta\nu_{fsr}} }} \end{aligned} \] 线宽 \[ \Delta\nu_c = \frac{\Delta\nu_{fsr}}{F} \]
精细度 \[ F=\frac{\pi r}{1-r^2} \]
PDH技术之前的激光锁定有些缺陷:无法区分激光频率的波动和激光器本身光强波动。
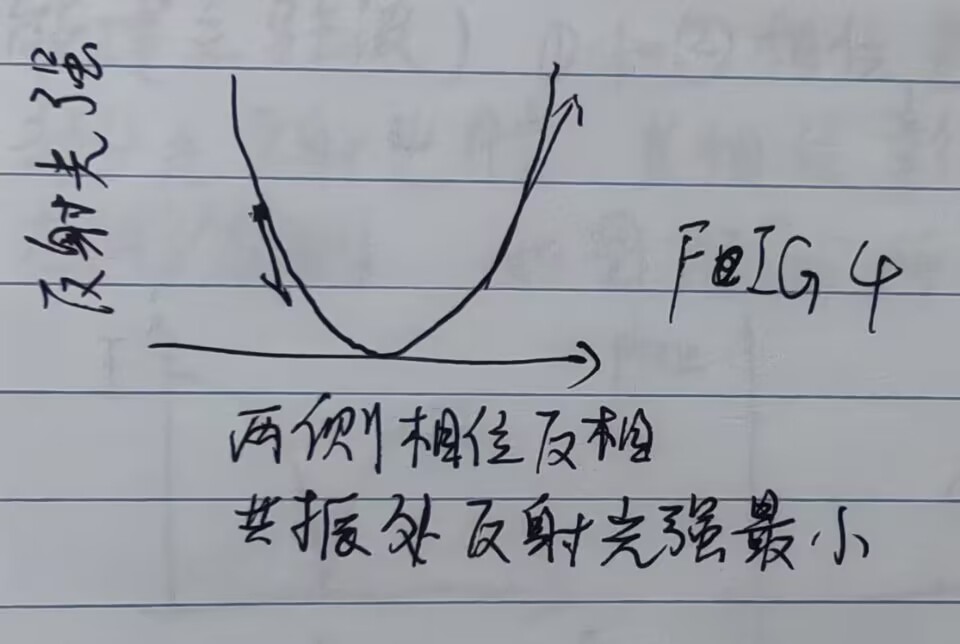
反射光强关于共振点对称,若不共振,无法区分频率是高于还是低于共振频率(通过观察反射光强的谱线)。注意到共振点两侧斜率(导数)有正负之分,可以用来区分,这个误差信号可以用来锁定激光。
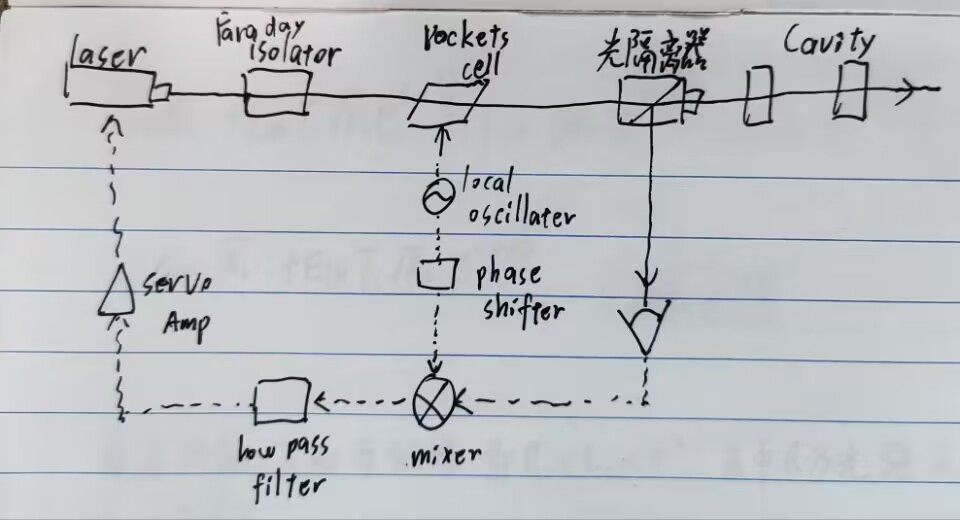
Pocket cell 泡克尔斯盒 用于电光相位调制\(E_{入} = A\cos wt,~~~~ E_{出} = A\cos (wt + \beta \sin w_mt)\),\(\beta\)为调制深度。
光隔离器由偏振分束PBS和\(\lambda/4\)波片组成。
反射光经过光隔离器打入光探测器,其输出与本地振荡器的信号通过混频器作比较,其输出包含直流(或低频)和两倍调制频率信号,我们要用低频成分计算误差并送入伺服系统控制反馈。
如果缓慢抖动激光频率,此概念模型可以生效。如果抖动太快,腔内共振光不能及时完全上升或下降,输出将不会按照FIG4显示。此PDH技术在高频调制下仍能工作,噪声和伺服系统的带宽都提高了,在解决在用于高频区的概念模型之前,可建立量化模型。
量化模型
A FP腔单色光的反射
FP腔反射光实际由两方面组成
- 快速反射光(被M反射后再没进入腔)
- 漏光(驻波在腔内往返过程中漏出的透射光)
这两种光有相同的频率,近共振(在无损对称腔中)其强度也几乎相同,但其相位严重依赖激光频率。
case 1 若完美共振,则\(\nu = N\cdot \Delta \nu_{fsr}\)
反射光中类型1和2有相同的振幅和相反相位,两光干涉相消,若反射光消失,即\(F(w)=0\)
case 2 若不完美共振,则\(\nu \neq N\cdot \Delta \nu_{fsr}\)
不完美指有小偏差。\(\nu\)与\(N\cdot \Delta \nu_{fsr}\)足够接近,能建立驻波。反射光中类型1和2的相位差不是180度,不会完全相消。部分光反射出腔,其相位彰显激光频率位于共振点左侧/右侧,如图FIG5所示。
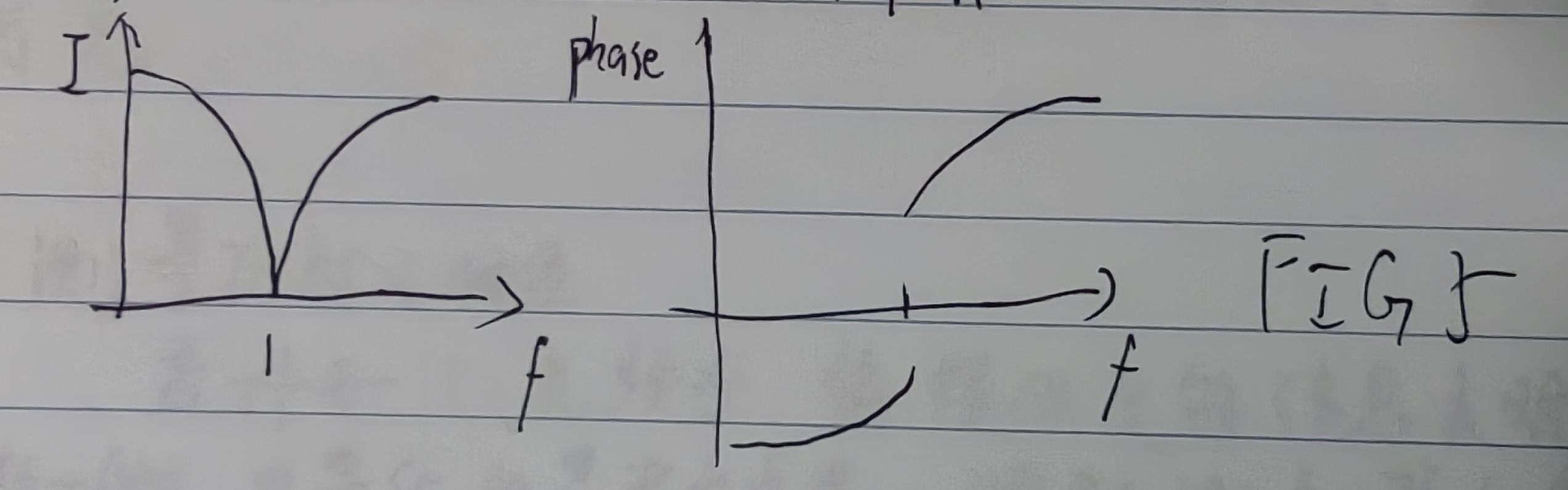
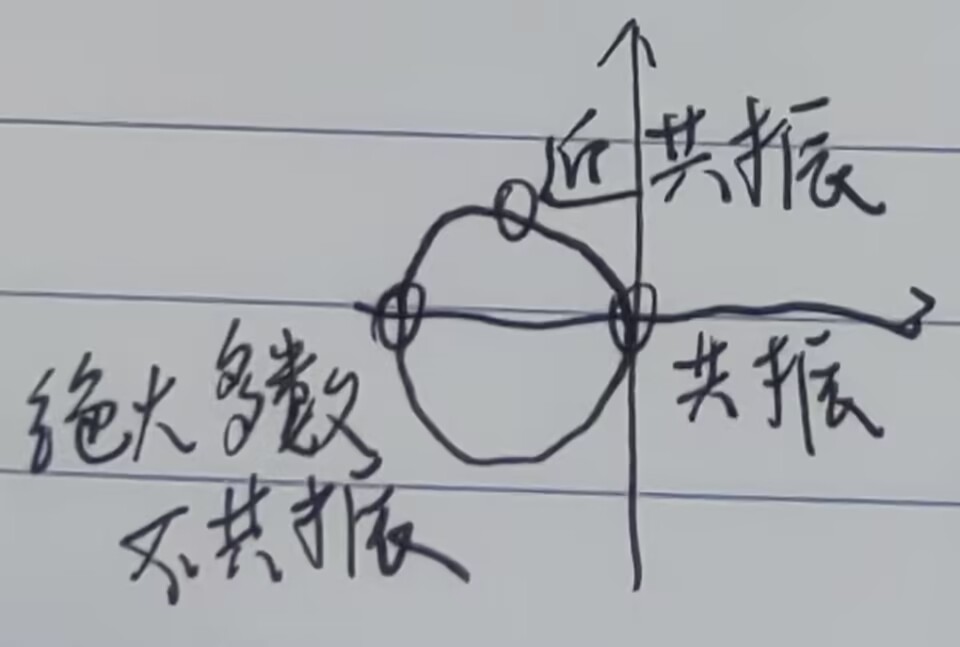
FIG6中,随着激光频率\(w\)增加,\(F(w)\)沿着园作逆时针运动(当\(w\)均匀增加的时候,函数在B点附近对\(w\)变化敏感,在A点附近对\(w\)变化不敏感)。 通过matlab模拟\(F(w)\)的复数值,大多数情况下靠近-1(A点)
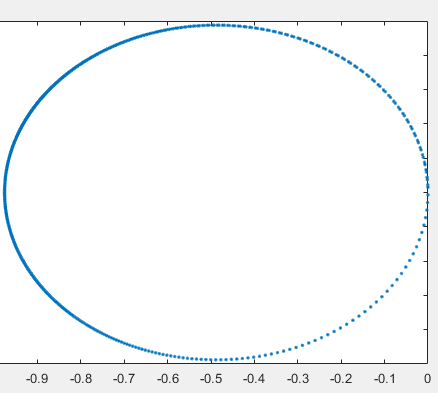

可见在近共振时,灵敏度较大
B 测量反射光相位
若抖动激光频率,将提供足够信息表明处于共振哪一侧,更量化的思考方式是,调制激光器的频率(或相位)将产生与入射光和反射光具有确定相位关系的边带,这些边带与入射光和反射光频率不同,但仍存在确定相位关系,若用反射光束干涉这些边带,则总和会显示调制频率下的拍频,拍频相位将告知反射光束的相位,边带设定了一个相位标准。通过该标准可以测量反射光束的相位。
C 调制激光:边带
量化模型中调制频率,实际中调制相位更容易,结果相同,但描述相位的数字方式更简单。通过pockets cell电光调制相位后,其入射电场变为
\[ E_{inc} = E_0 e^{i(wt + \beta \sin \Omega t)}~~~~ \Omega 是调制频率, ~~~~ \beta 是调制深度 \]
用贝塞尔函数展开
\[ \begin{aligned} E_{inc} &\approx [J_0(\beta) + 2\sigma J_1(\beta)\sin \Omega t]e^{iwt} \cdot E_0 \\ &= E_0 [J_0(\beta)e^{iwt} + J_1(\beta)e^{i(w+\Omega)t} - J_1(\beta)e^{i(w-\Omega)t}] \end{aligned} \]
若\(P_0 = |E_0|^2\)是入射光总功率,忽略干涉效应\(P_c = J_0^2(\beta)P_0\)
一阶边带功率\(P_s = J_1^2(\beta)P_0\)。当\(\beta < 1\)时,\(P_c + 2P_s \approx P_0\)
D 调制信号的反射:误差信号
\[ \begin{aligned} E_{ref} &= E_{in}\cdot F(w) \\ &= E_0[F(w)J_0(\beta)e^{iwt} + F(w + \Omega)J_1(\beta)e^{i(w+\Omega)t} - F(w-\Omega)J_1(\beta)e^{i(w-\Omega)t}] \end{aligned} \]
由于光电二极管作为误差信号探测器,实际上测量的是光强\(P_{ref} = |E_{ref}^2|\),故光电二极管起到一个混频器的作用,每项与另外两项混频得到
\[ P_{ref} = |E_{ref}|^2 = E_{ref} \cdot E_{ref}^* \]
\(P_c = E_0^2J_0^2(\beta)~~~~P_s = E_0^2J_1^2(\beta)\)
\[ E_{ref} = E_0[F(w)J_0(\beta)e^{iwt} + F(w + \Omega)J_1(\beta)e^{i(w+\Omega)t} - F(w-\Omega)J_1(\beta)e^{i(w-\Omega)t}] \] \[ E_{ref}^* = E_0[F^*(w)J_0(\beta)e^{iwt} + F^*(w + \Omega)J_1(\beta)e^{i(w+\Omega)t} - F^*(w-\Omega)J_1(\beta)e^{i(w-\Omega)t}] \]
所以
\[ \begin{aligned} P_{ref} &= |E_{ref}|^2 = E_{ref} \cdot E_{ref}^* \\ &= E_0^2 |F(w)|^2J_0^2(\beta) + E_0^2 F(w+\Omega)F^*(w+\Omega)J_1^2(\beta) \\ &~~~~+ E_0^2 F(w-\Omega)F^*(w-\Omega)J_1^2(\beta) + E_0^2 F(w)F^*(w+\Omega)J_0(\beta)J_1(\beta)e^{-i\Omega t} \\ &~~~~- E_0^2 F(w)F^*(w-\Omega)J_0(\beta)J_1(\beta)e^{i\Omega t} + E_0^2 F^*(w)F(w+\Omega)J_0(\beta)J_1(\beta)e^{i\Omega t} \\ &~~~~- E_0^2 F(w+\Omega)F^*(w-\Omega)J_1^2(\beta)e^{2i\Omega t} - E_0^2 F^*(w)F(w-\Omega)J_0(\beta)J_1(\beta)e^{-i\Omega t} \\ &~~~~- E_0^2 F(w-\Omega)F^*(w+\Omega)J_1^2(\beta) e^{-2i\Omega t} \\ &= P_c|F(w)|^2 + P_s \{ |F(w + \Omega)|^2 + |F(w-\Omega)|^2 \} \\ &~~~~ +[F(w)F^*(w+\Omega) - F^*(w)F(w-\Omega)]E_0^2J_0(\beta)J_1(\beta)e^{-i\Omega t} \\ &~~~~ +[F^*(w)F(w+\Omega) - F(w)F^*(w-\Omega)]E_0^2J_0(\beta)J_1(\beta)e^{i\Omega t} + ~~其余2\Omega 项 \end{aligned} \]
设\(F(w)F^*(w+\Omega)=a+bi\)
则\(F^*(w)F(w+\Omega)=a-bi\)
原式变为 \[ P_{ref} = P_c|F(w)|^2 + P_s \{ |F(w + \Omega)|^2 + |F(w-\Omega)|^2 \} + E_0^2J_0(\beta)J_1(\beta)[ (a+bi)e^{-i\Omega t} + (a-bi)e^{i\Omega t} ] \]
而 \[ \begin{aligned} &(a+bi)e^{-i\Omega t} + (a-bi)e^{i\Omega t} \\ &= (a+bi)(\cos \Omega t - i \sin \Omega t) + (a-bi)(\cos\Omega t + i\sin\Omega t) \\ &= 2a\cos \Omega t + 2b\sin \Omega t \end{aligned} \]
所以 \[ P_{ref} = P_c|F(w)|^2 + P_s \{ |F(w + \Omega)|^2 + |F(w-\Omega)|^2 \} + 2\sqrt{P_c P_s}( a\cos \Omega t + b\sin \Omega t ) \]
我们只对\(\cos \Omega t\)或\(\sin \Omega t\)感兴趣,因为其反映了相移
- 若调制频率很小(\(\Omega \ll \Delta \nu_c\)),则\(F(w)F^*(w+\Omega) - F^*(w)F(w-\Omega)\)为实数,正弦项为0,留住余弦项。
- 若调制频率很大(\(\Omega \gg \Delta \nu_c\)),则\(F(w\pm \Omega) \approx -1,~~~~ F(w)F^*(w+\Omega) -F*(w)F(w-\Omega)\)为虚数,余弦项为0,留正弦项。
证明:
当\(\Omega\)很小,用泰勒公式展开,保留前两项
\(F(w)F^*(w+\Omega) - F^*(w)F(w-\Omega)\)
\(=F(w)(F^*(w) + \frac{dF^*(w)}{dw} \cdot \Omega) - F^*(w)(F(w) - \frac{dF(w)}{dw} \cdot \Omega)\)
\(=[F(w)\frac{dF^*(w)}{dw} + F^*(w)\frac{dF(w)}{dw}] \Omega\)
\(= \frac{d[F(w)F^*(w)]}{dw} \Omega =\frac{d|F|^2}{dw}\Omega\)
结果为实数
通过matlab计算,当\(\Omega \gg \Delta \nu_c\)时,确实有\(F(w\pm \Omega) \approx -1\),众多值集中在复平面(FIG6)的A点,故
\(F(w)F^*(w+\Omega) - F^*(w)F(w-\Omega) = -2bi = -i \cdot 2Im[F(w)]\)
结果为虚数
取正弦或余弦的一次分量,可通过使用混频器与滤波器来实现。
如果输入信号都是sin,那么\(\sin(\Omega t)\sin(\Omega' t) = 1/2 \{ \cos[(\Omega - \Omega')t] - \cos[(\Omega + \Omega')t] \}\)。若\(\Omega = \Omega'\),则\(\cos(\Omega - \Omega')t\)为直流分量,正是我们需要的,可以用一个低通滤波器滤除\(\cos(\Omega + \Omega')t\)而保留\(\cos(\Omega - \Omega')t\)
如果输入信号是sin和cos,那么\(\sin(\Omega t)\cos(\Omega' t) = 1/2 [\sin(\Omega - \Omega' t) - \sin(\Omega + \Omega')t]\) 当\(\Omega = \Omega'\),\(\sin(\Omega - \Omega')t=0\)无意义。故需要注意混频器两端输入信号相位,使混频器项均为正弦项。实际上,由于不同系统输入到混频器两端的信号相位不同,往往在混频器前加一个可调移相器,以便混频时能使两信号相位适配。
理解量化模型
A 慢调制概念模型的量化
当驻波锁定时,\(w\)是一个定值,在未锁定时,\(w\)会有一个变化的漂移范围,是一个变量。用\(w(t)\)表示。即\(w(t)\)缓慢抖动
\[ E_{in} = E_0 \cos(wt + \beta \sin \Omega t) \]
相位是\(wt + \beta \sin \Omega t\),则瞬时频率\(w(t) = \frac{d\phi}{dt} = \frac{d(wt + \beta \sin \Omega t)}{dt} = w+\Omega\beta\cos\Omega t\)
慢调制下\(\Omega \approx 0\)
\[ P_{ref} = P_0|F(w)|^2 \]
\[ \begin{aligned} P_{ref}(w + \Omega\beta\cos\Omega t) &\approx P_ref(w) + \frac{dP_ref}{dw} \cdot \Omega\beta \cos \Omega t \\ &\approx P_ref(w) + P_0\frac{d|F(w)|^2}{dw} \cdot \Omega\beta\cos\Omega t \end{aligned} \]
概念模型中,在隔热环境下缓慢抖动激光频率w,使腔内驻波总是与入射光束相均衡,在量化模型中可用很小的\(\Omega\)表达
前面证明了\(F(w)F^*(w+\Omega) - F^*(w)F(w-\Omega) = \frac{d|F(w)|^2}{dw}\cdot \Omega\)是实数,只有余弦项。若我们使\(\sqrt{P_c P_s}\)约等于\(P_0\beta / 2\)
那么\(P_{ref} = 常数项 + P_0\frac{d|F(w)|^2}{dw} \cdot \Omega\beta\cos\Omega t + (2\Omega 项)\)
量化模型与概念模型抑制,混频器会消除除\(\cos\Omega t\)之外的其余项
PDH误差信号\(\varepsilon = P_0\frac{d|F(w)|^2}{dw}\Omega\beta \approx 2\sqrt{P_c P_s}\frac{d|F(w)|^2}{dw}\Omega\) 其中\(|F(w)|^2\)表征输出光强,\(\frac{d|F(w)|^2}{dw}\)可表示光强I随\(w\)变化的导数,在共振两侧,导数有正负之分,在误差图中\(\varepsilon\)有正负之分。
B 近共振快调制,实操中的PDH
当\(w\)近共振,即\(w\approx 2\pi N\Delta \nu_{fsr}\),调制频率\(\Omega\)很高,边带消失。假设边带被完全反射,\(F(w\pm \Omega) \approx -1\),由于近共振,则\(F(w)\approx 0\) \(F(w)F^*(w+\Omega) - F^*(w)F(w-\Omega) \approx -i\cdot 2 Im{F(w)}\),证明见前文。
所以\(P_{ref} \approx 2P_s - 4\sqrt{P_c P_s} Im{F(w)}\sin\Omega t + 2\omega 项\)
\(\varepsilon \approx -4\sqrt{P_c P_s}Im{F(w)}\)
由于近共振 \[ \frac{w}{\Delta \nu_{fsr}} = 2\pi N + \frac{\delta w}{\Delta \nu_{fsr}} ~~~~ \delta w是w偏离共振频率的偏量,N是整数 \]
若腔的精细度很高\(F\approx \frac{\pi}{1-r^2}~~~~r\approx 1\) \[ \frac{\delta w}{\Delta \nu_{fsr}} = \frac{\delta w}{\Delta \nu_c \mathcal{F}} \]
\[ F(w) = \frac{ r(e^{i\frac{\delta w (1-r^2)}{\Delta \nu_c \pi }} \cdot e^{i2\pi N} - 1) }{1 - r^2 e^{i\frac{\delta w (1-r^2)}{\Delta \nu_c \pi }}\cdot e^{i2\pi N} } \]
由于 \[ e^{i2\pi N} = 1 , ~~~~ r \approx 1, ~~~~ \delta w很小 \]
所以 \[ F(w) = \frac{ i\delta w }{ \Delta \nu_c \pi } \]
带入误差信号公式 \[ \varepsilon \approx - \frac{ 4 }{ \pi } \sqrt{ P_c P_s } \cdot \frac{ \delta w }{ \delta \nu_c } ~~~~ \delta \nu_c = \frac{ \Delta \nu_{fsr} }{ \mathcal{F} }线宽 \]
误差信号\(\varepsilon\)正比于\(\delta w\),只要\(\delta w \ll \delta \nu_c\),上式就会成立。误差信号是线性近共振的,能用线性控制理论来抑制频率噪声。
用\(f = \nu = \frac{ w }{ 2\pi }\)来代替更符合习惯
\[ \varepsilon = -8\sqrt{ P_c P_s } \cdot \frac{ \delta f }{ \delta \nu_c } ~~~~ \varepsilon = D \cdot \delta f ~~~~ D = -\frac{ 8\sqrt{ P_c P_s } }{ \delta \nu_c } \]
思考与理解
(A)慢调制中,\(w(t) = w + \Omega\beta \cos \Omega t\)表征了频率抖动与调制频率\(\Omega\)的关系。即中心频率为\(w\),以\(\Omega\beta\)为振幅的余弦波动
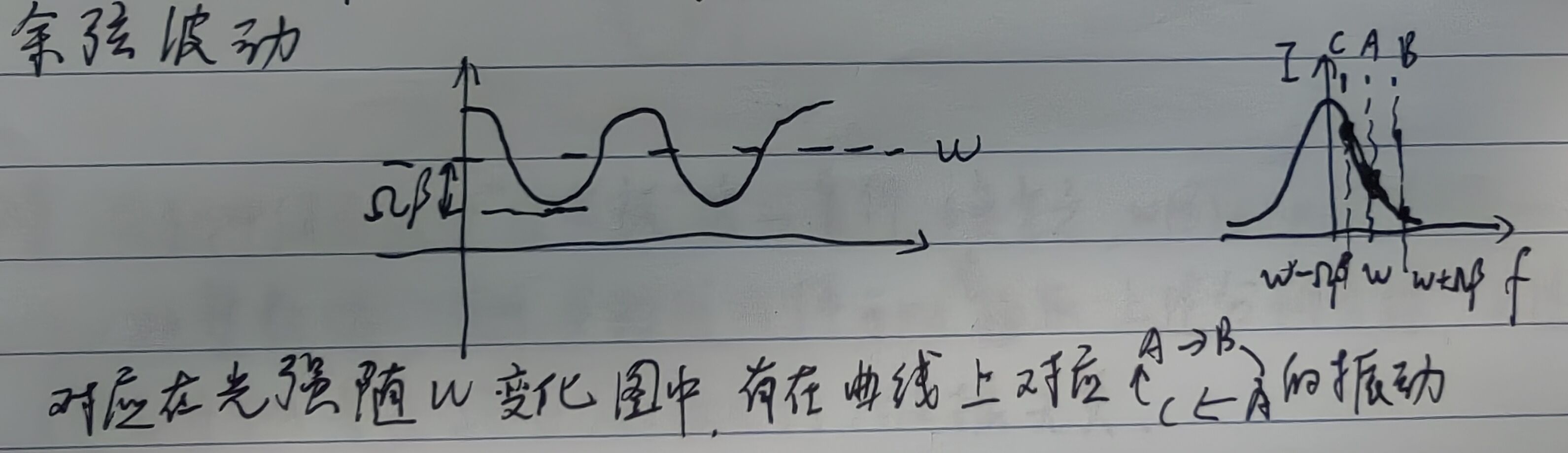
对应在光强随\(w\)变化图中,有在在曲线上对应A->B->A->C->A的振动
功率\(P_{ref}(w + \Omega\beta\cos \Omega t) \approx P_{ref}(w) + P_0\frac{d|F|^2}{dw} \Omega \beta \cos \Omega t\)其中\(w\)为中心频率,即\(w_A\)
从A到B过程中:\(\cos\Omega t > 0 ~~~~ \frac{ d|F|^2 }{ dw } < 0 ~~~~~ P_B < P_A\)
从A到C过程中:\(\cos\Omega t < 0 ~~~~ \frac{ d|F|^2 }{ dw } < 0 ~~~~~ P_C > P_A\)
上述为\(w \neq 2\pi N \Delta \nu_{fsr}\)的情形 若\(w = 2\pi N \Delta \nu_{fsr}\),即近共振时
从A到B过程中:\(\cos\Omega t > 0 ~~~~ \frac{ d|F|^2 }{ dw } < 0 ~~~~~ P_B < P_A\)
从A到C过程中:\(\cos\Omega t < 0 ~~~~ \frac{ d|F|^2 }{ dw } > 0 ~~~~~ P_C < P_A\)
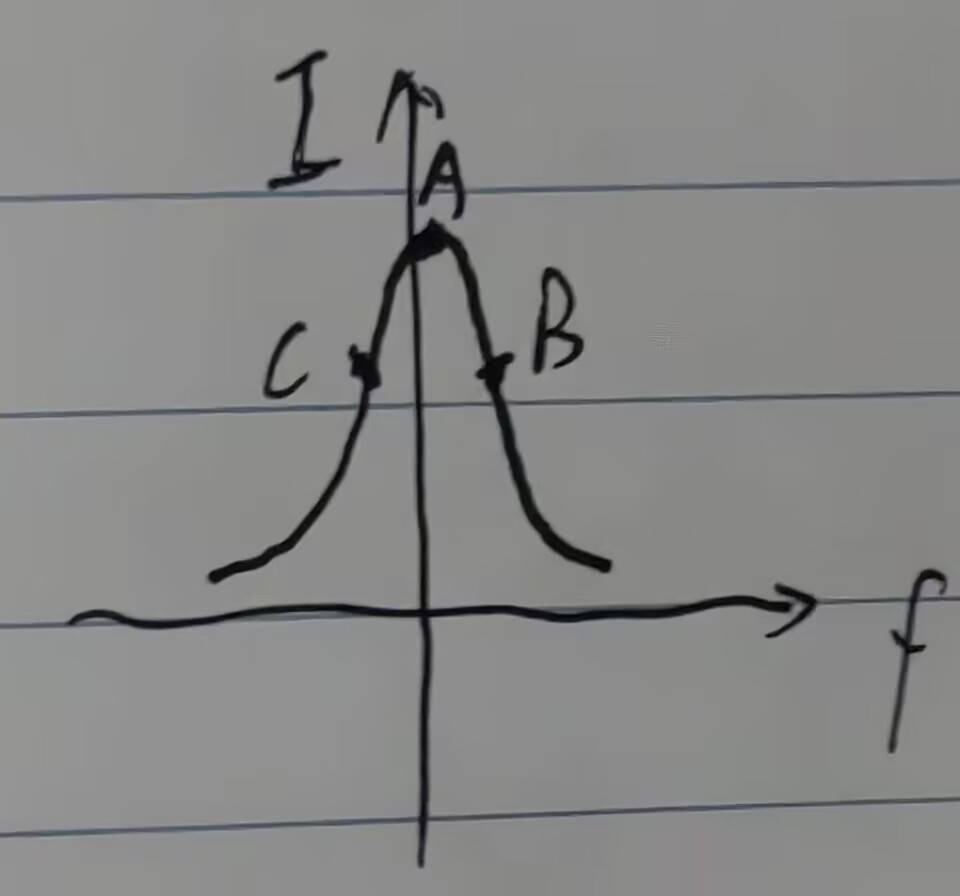
其误差信号 \[ \varepsilon = P_0 \frac{ d|F|^2 }{ dw } \Omega \beta \approx 2\sqrt{ P_c P_s } \frac{ d|F|^2 }{ dw } \Omega \]
注意在把误差信号送入混频器前必须调整其相位(-90度)
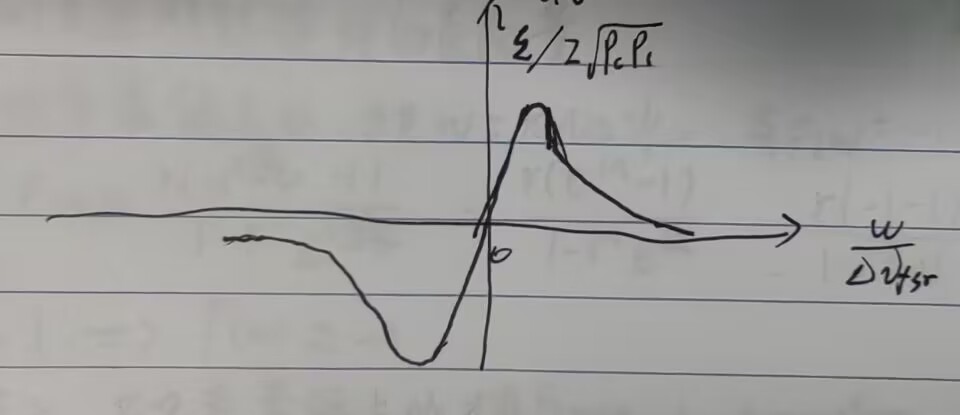
慢调制中没有规定“近共振”这一条件,换言之,\(w(t)\)的中心频率\(w\)不是\(\Delta \nu_{fsr}\)的整数倍。不近共振同样可以采取上述分析方法,上述方法中的近似是在\(\Omega \approx 0\)时进行,与共振无关。
(B)块调制中,有个前提就是“近共振”。在这一条件下,有诸多近似关系: \[ F(w) \approx 0 ~~~~ w \approx 2\pi N \Delta \nu_{fsr} \]
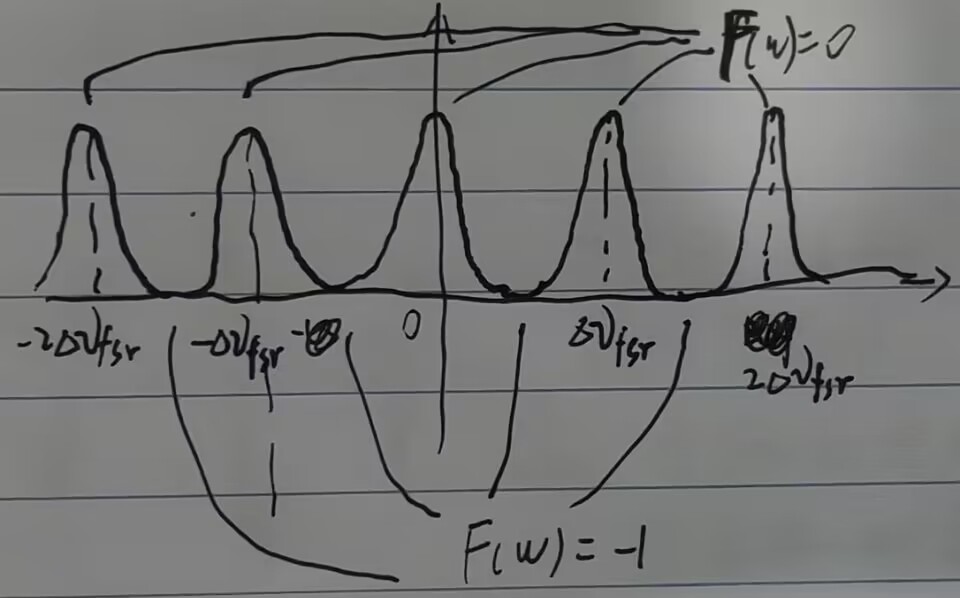
由于\(F(w)\)是逆时针旋转的直向量 功率最低点处,\(w = \pi N \Delta \nu_{fsr}\),有\(F(w) = -1\),其中\(N\)为奇数。
事实上,不只有最低点处才有\(F(w)\approx -1\),由matlab可知\(F(w)\)在绝大多数情况下均可以近似为-1。而\(F(w)=-1\)的物理意义是该频率的光没有在腔内形成共振,被完全反射出腔外。
非近共振光的确只要不满足\(\nu = \frac{ C }{ 2L } q\)就无法在腔内共振,只有在近共振情形下,复平面的圆才会有较为可观虚部的\(F(w)\)
由误差信号公式\(\varepsilon = D\delta f\)不难看出\(\varepsilon\)是与\(\delta f\)成比例的正比例函数。由于该式是在\((\delta w \ll \delta \nu_c)\)的前提下推导出来的,在图中只表现为共振处附近的斜线,其余部分是非线性的,与\(\varepsilon = D\delta f\)无关。我们只关注线性部分的变化
