通信笔记4
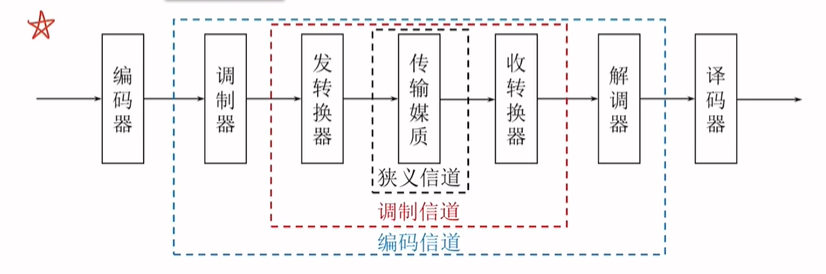
信道
定义:以传输媒质为基础的信号通道
狭义信道
- 有线信道 同轴电缆,光纤等
- 无线信道 微波视距传播,卫星中继,移动通信等
广义信道
- 调制信道 研究调制解调问题
- 编码信道 研究编码译码问题
恒参信道:信道传输特性随时间缓慢变化或不变化的信道。比如各种有线信道
随参信道:信道传输特性随时间随机快速变化的信道。比如短波电离层反射,各种散射,移动通信等信道
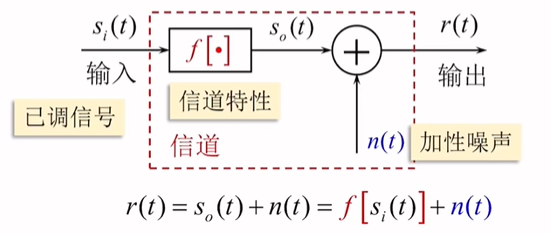
调制信道
调制信道的特点
- 有一对/多对输入/输出端
- 大多满足线性叠加原理
- 对信号有固定或时变的延迟(相位)和损耗(幅值)
- 无信号输入,仍有可能输出,此时输出噪声
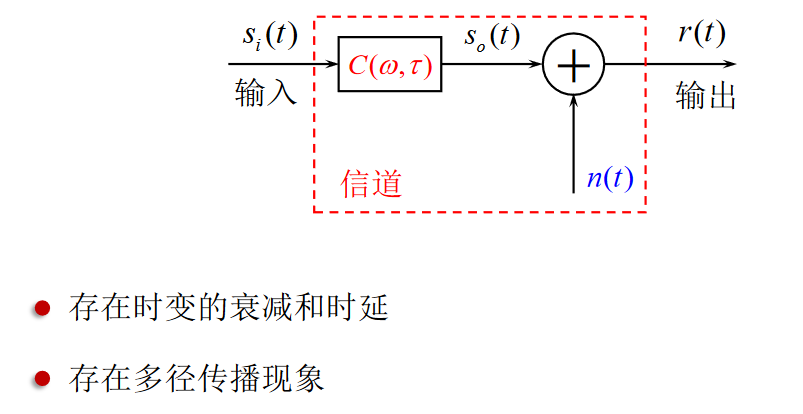
调制信道的数学模型:叠加有噪声的线性时不变/时变滤波器
恒参信道对应线性时不变滤波器\(c(t) <==> C(w)\),随参信道对应线性时变滤波器\(c(t,\tau) <==> C(w,\tau)\)
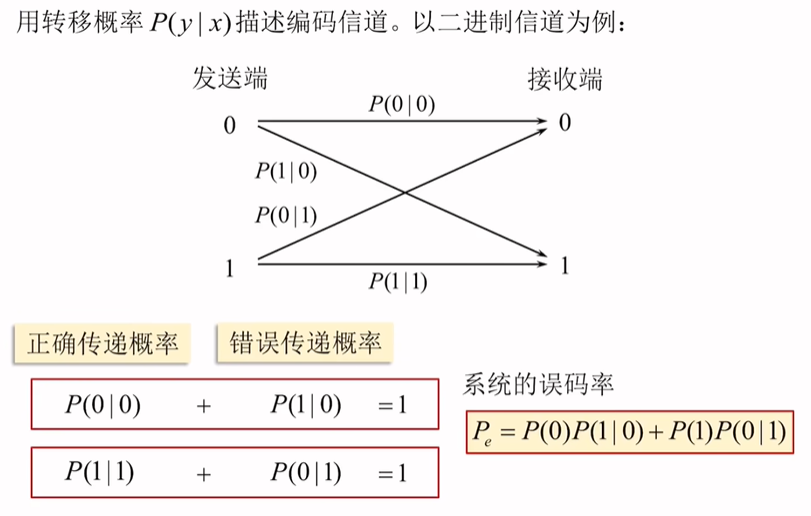
编码信道
编码信道数学模型
编码信道分类:无记忆信道(前后码元发生的错误相互独立),有记忆信道(一个码元发生错误和前后码元有依赖关系,使用马尔可夫链描述)
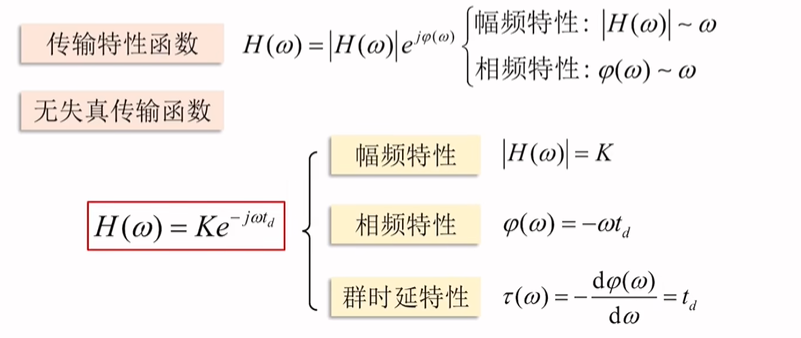
理想恒参信道
理想无失真传输信道可以等效为一个线性时不变网络
理想恒参信道满足无失真传输条件,即输入输出波形结构一致,只是幅度和出现时间不同
系统输入输出管旭和冲击响应
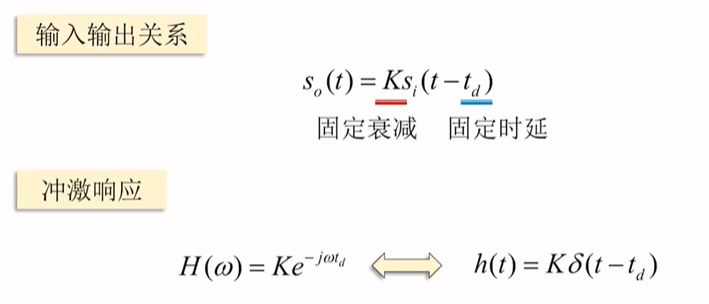
失真
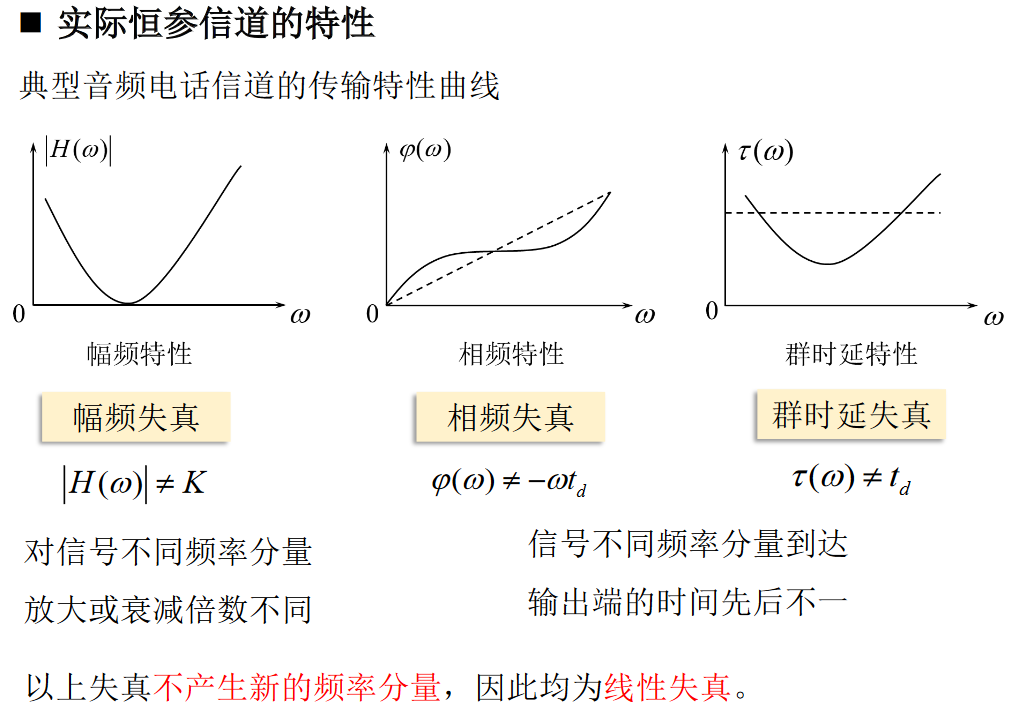
幅频失真对信号的影响
- 幅频失真对模拟信号的影响:发生波形失真,导致信噪比下降
- 幅频失真对数字信号的影响:发生码间干扰,导致误码率增大
相频失真对信号的影响
- 相频失真对模拟信号的影响:对语音信号影响不大(人耳不易分辨),对视频信号影响大
- 相频失真对数字信号的影响:发生码间干扰,导致误码率增大
改善线性失真的措施:采用均衡技术:向无失真传输特性靠拢
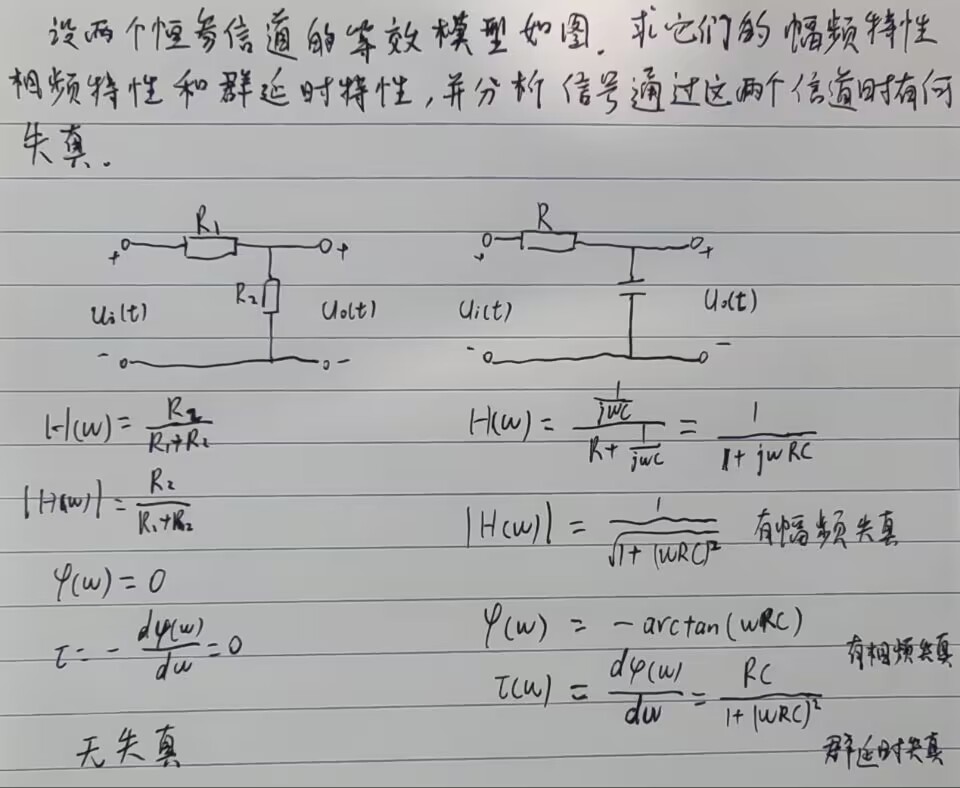
例题
随参信道
随参信道特性
多途径传播影响
\[ s(t) = A\cos(w_c t) ~~~~ ==> ~~~~ r(t) = \sum_{i=1}^n a_i(t)\cos(w_c(t - \tau_i(t) )) \]
其中\(r(t)\)是包络和相位随机缓慢变化的窄带信号。\(a_i(t)\)是时变衰弱,\(\tau_i(t)\)是时变时延
把\(r(t)\)拆解成同相分量和正交分量:
\[ \begin{aligned} r(t) &= \sum_{i=1}^n a_i(t)\cos(w_c t - \phi_i(t) ) ~~~~ \phi_i(t) = w_c\tau_i(t) \\ &= \sum_{i=1}^n a_i(t) \cos \phi_i(t) \cos w_c t - \sum_{i=1}^n a_i(t) \sin \phi_i(t) \sin w_c t \\ &= X(t)\cos w_c t - Y(t) \sin w_c t \\ &= V(t)\cos [w_c t + \phi (t)] \end{aligned} \]
\[ V(t) = \sqrt{ X(t)^2 + Y(t)^2 }, ~~~~ \phi(t) = \arctan \frac{Y(t)}{X(t)} \]
多径传播影响:
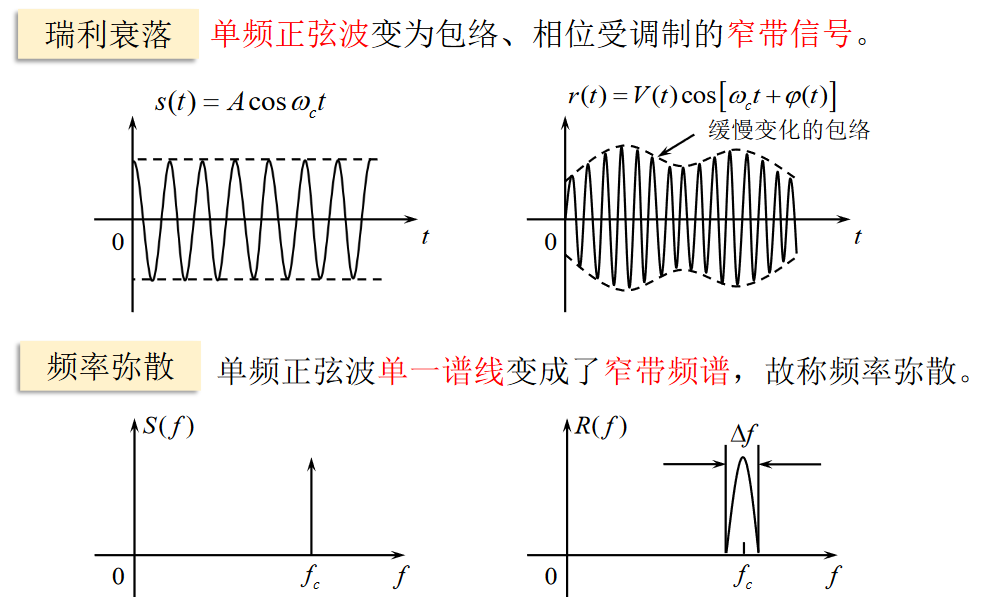
两径传播模型:
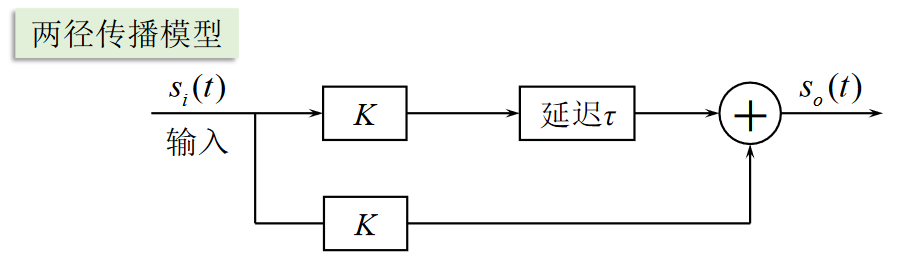
\[ s_o(t) = Ks_i(t) + Ks_i(t-\tau) \] \[ S_o(w) = KS_i(w) + KS_i(w)e^{-jw\tau} = KS_i(w)(1 + e^{-jw\tau}) = 2K\cos \frac{w\tau}{2} e^{ -j\frac{w\tau}{2} } \]
幅频特性 \[ \left| H(w) \right| = 2K \left| \cos \frac{w\tau}{2} \right| \] 频率选择性衰弱:信道对不同频率的信号成分有不同的衰减,且随时间变化,这种现象称为频率选择性衰落。
信道相关带宽:
相邻传输零点的频率间隔为信道相关带宽\(\Delta f = \frac{1}{\tau}\)
为避免频率选择性衰落,应使信号带宽满足 \(B_s < \Delta f\)
工程上一般选取\(B_s = \left( 1/5 \sim 1/3 \right) \Delta f\) 码元宽度满足\(T_B = (3\sim 5)\tau\)
两径推广至多径
\(\tau_{max}\)为最大的路径时延差 \[ \Delta f = \frac{1}{\tau_{max}} \]
解决方法:OFDM技术
将信道划分为N个正交子信道,从而将高速的串行数据信号划分为N路并行的低速子数据流,分别调制到各路的载波上并行传输,从而使码长变大,带宽减小,并小于信道的相关带宽。
频率选择性衰落的解决方法:
分集接收、扩频、MIMO、均衡等
将接收到的信号按照一定的分集方式分离成不相关的多路信号,然后再按照一定的规则合并,目的是最大化接收信号能量,提高信号的载噪比。
常见的分集方式有空间分集、频率分集、角度分集、极化分集等; 常见的合并方式有最佳选择式、等增益相加式、最大比值相加式等。
噪声与带宽
分类:
- 按噪声来源分类
- 人为噪声、自然噪声、内部噪声(如热噪声)等。
- 按噪声性质分类
- 脉冲噪声、窄带/单频噪声、起伏噪声等。
其中起伏噪声对信号干扰最为严重,包含热噪声、散弹噪声、宇宙噪声等。
热噪声定义:零均值高斯白噪声
热噪声三个特点
- 来自一切电阻性元器件中电子的热运动
- 其功率谱均匀分布在\(0 \sim 10^{12}Hz\)频率范围内,可视为白噪声
- 其电压瞬时值服从高斯分布,且均值为0
信道加性噪声:典型的信道加性噪声代表是起伏噪声(热噪声等),它是零均值的高斯白噪声。
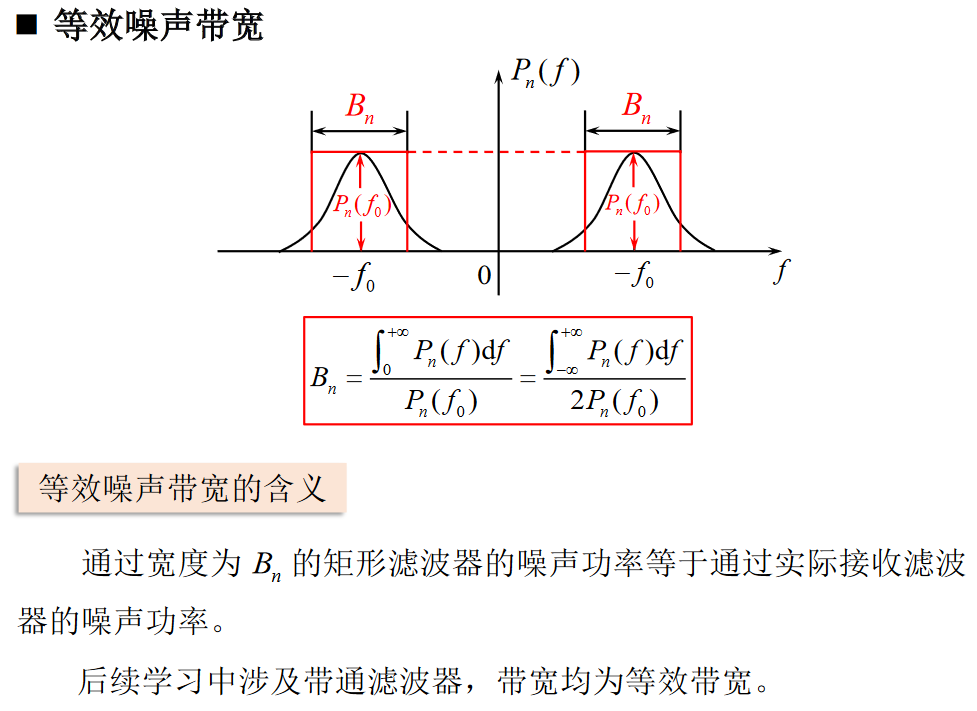
等效噪声带宽(在功率谱面积上等效):
信道容量
离散信道容量
离散信道容量有两种不同的单位
- 用每个符号(symbol)能够传输的平均信息量最大值表示信道容量\(C\)
- 用单位时间(秒)内能够传输的平均信息量最大值表示信道容量\(C_t\)
二者可以互换
借助书本《通信原理(第七版)》P79图4-24 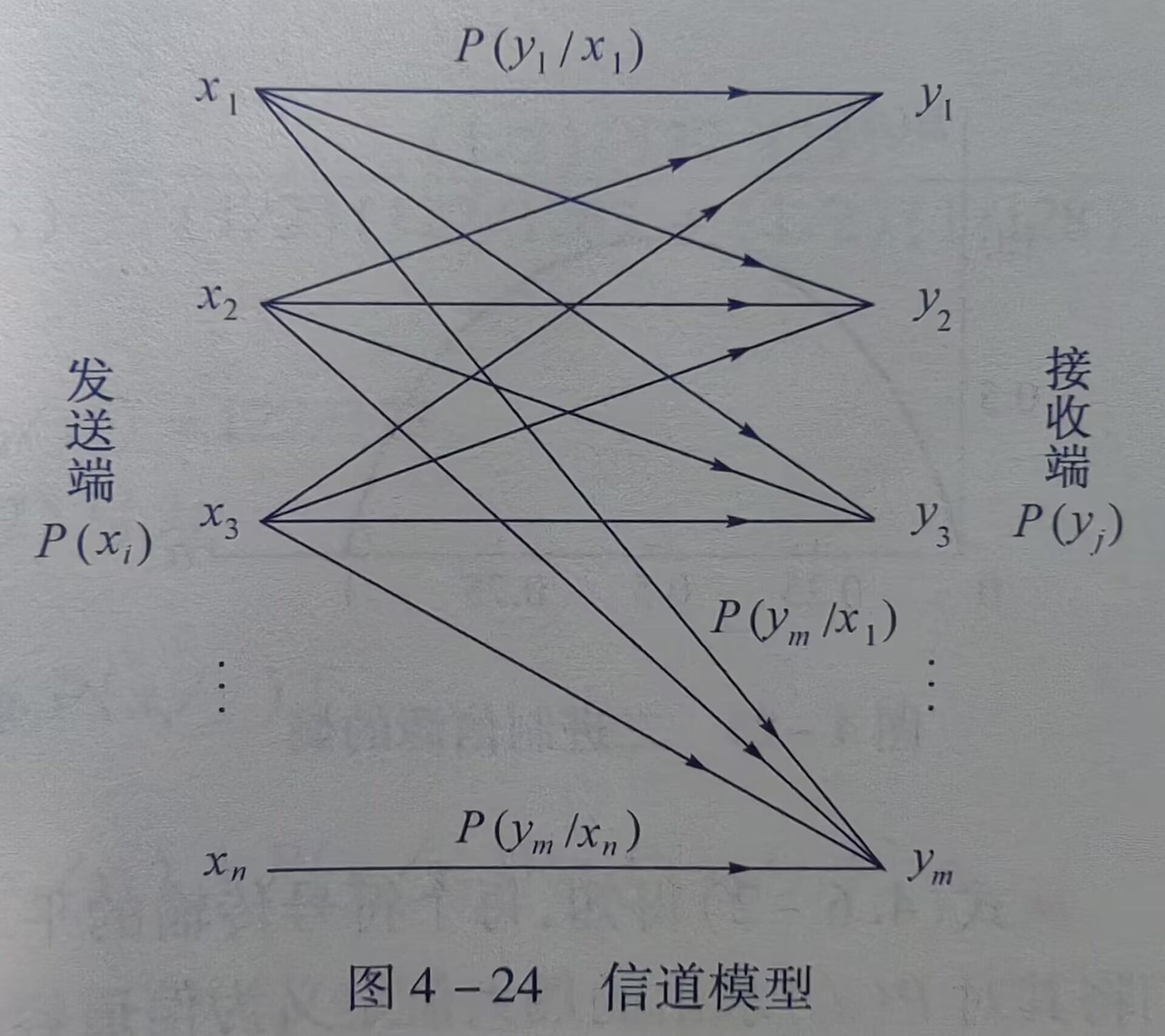
图中发送符号\(x_1, x_2, x_3, \cdots x_n\)的出现概率为\(P(x_i), i=1,2,\cdots n\);收到\(y_i\)的概率是\(P(y_j), j=1,2,\cdots m\)。
\(P(y_j/ x_i)\)是转移概率,即发送\(x_i\)条件下收到\(y_j\)的条件概率。
发送\(x_i\)到\(y_j\)所获得的信息量等于发送\(x_i\)前接收端对\(x_i\)的不确定程度(\(x_i\)的信息量)减去收到\(y_j\)后接收端对\(x_i\)的不确定程度(给定\(y_j\)条件下\(x_i\)的不确定程度),即发送\(x_i\)时收到\(y_j\)所获得的信息量\(~ = -\log_2 P(x_i) - [ -\log_2 P(x_i/y_j) ]\)对所有\(x_i,y_j\)取统计平均值,得出收到一个符号时获得的平均信息量: \[ \begin{aligned} 平均信息量/符号 &= - \sum_{i=1}^n P(x_i)\log_2 P(x_i) - \left[ - \sum_{j=1}^m P(y_j) \sum_{i=1}^n P(x_i/y_j)\log_2 P(x_i/y_j) \right] \\ &= H(x) - H(x/y) \end{aligned} \tag{1} \]
式(1)中\(H(x)\)是发送符号\(x_i\)的平均信息量,称为信源的熵。\(H(x/y)\)是接收\(y_j\)已知后,发送\(x_i\)的平均信息量
对于二进制信源,假设发送1的概率为\(P(1) = \alpha\),那么发送0的概率为\(P(1) = 1- \alpha\) \[ H(\alpha) = -\alpha \log_2 \alpha - (1-\alpha) \log_2 (1 - \alpha) \tag{2} \] 按式(2)绘制曲线,当两个符号出现概率相等(\(\alpha = 0.5\)),不确定性最大,信息量最多,对应通信笔记1中“等概率离散消息度量”有关内容。
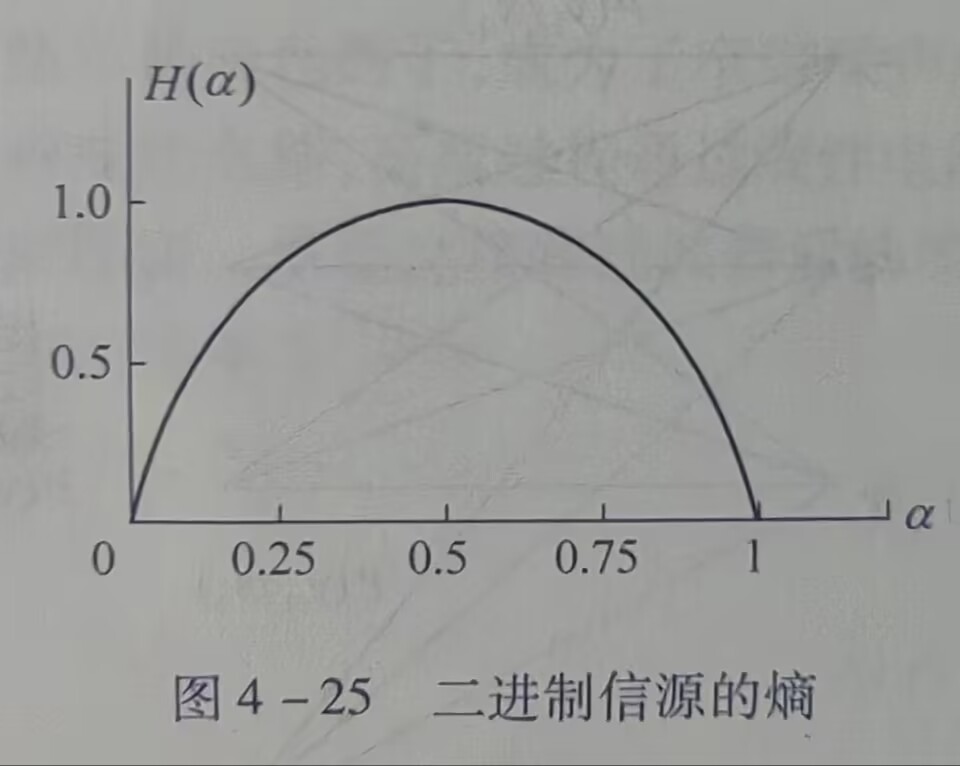
没有噪声时,\(H(x/y)=0\)
每个符号传输的平均信息量和信源发送符号概率\(P(x_i)\)有关。\(H(x) - H(x/y)\)对\(P(x_i)\)求最大值得到信道容量\(C\) \[ C = \max_{P(x)} [H(x) - H(x/y)] ~~~~ b/符号 \]
设单位时间内传输符号个数\(r~~ 符号/s\)
\[ C_t = \max_{P(x)} { r[ H(x) - H(x/y) ] } ~~~~ b/s \]
直接拍一张例题理解一下吧,我懒得码字了[doge] 
连续信道容量
直接放公式 \[ C_t = B\log_2 (1 + \frac{S}{N}) = B\log_2 (1 + \frac{S}{n_0 B}) = \frac{S}{n_0} \log_2 (1+x)^{1/x} ~~~~ b/s \] \(S\)是信号平均功率,\(N\)是噪声功率,\(B\)是带宽,\(n_0\)是噪声功率谱密度
设\(E_b=ST_b\)是每比特能量,\(T_b=\frac{1}{B}\)是每比特持续时间。 \[ C_t = B\log_2 (1 + \frac{ E_b/T_b }{n_0 B}) = B\log_2 (1 + \frac{ E_b }{n_0}) \]
再来拍一张例题理解一下
