通信笔记5
模拟调制与解调
调制:把消息信号寄托在载波的某个参数上,形成已调信号。
解调:调制的逆过程,从已调信号中恢复消息信号。
调制目的:
- 匹配信道特性,减小天线尺寸,提高辐射效率
- 通过频谱搬移,实现信道的多路复用,提高信道利用率
- 拓展信号带宽,提高抗干扰能力
- 实现带宽与信噪比的互换
调制分类
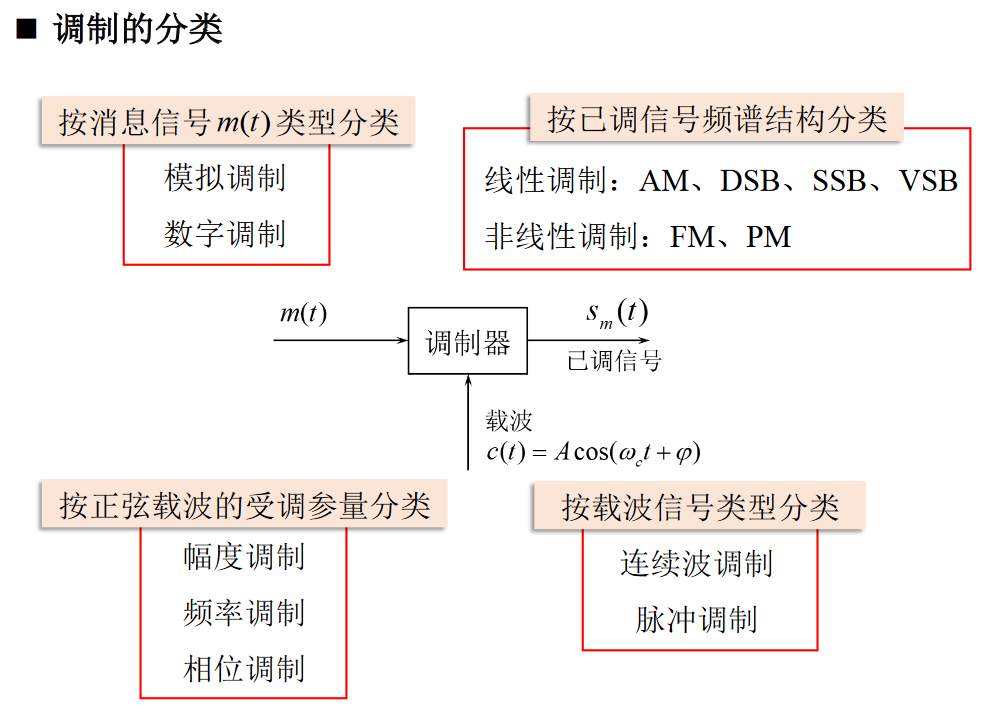
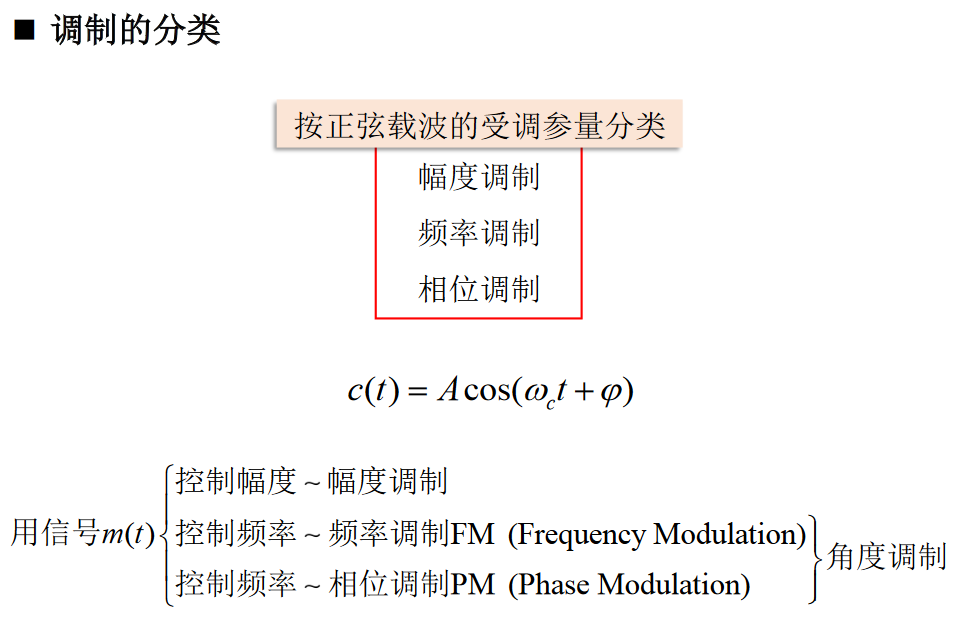
线性调制
调幅AM
AM调制原理图
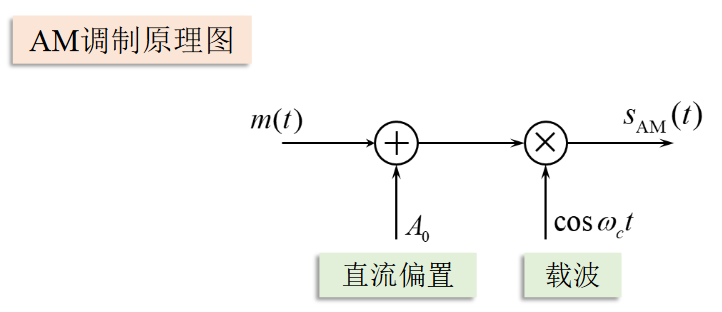
其中\(m(t)\)均值为0,且直流偏置\(A_0 \geq |m(t)|_{max}\)
AM调幅系数: \[ a = \frac{ |m(t)|_{max} }{ A_0 } \]
当调制系数小于等于1时,包络和\(m(1)\)成正比,可以用包络检波进行解调。当调制系数大于1时,调制信号会出现载波反向点,包络和\(m(1)\)不成正比。
调制信号的时域表达式
\[ s_{AM}(t) = [A_0 + m(t)] \cos w_c t = A_0 \cos w_c t + m(t) \cos w_c t \]
\(A_0 \cos w_c t\)为载波项,\(m(t) \cos w_c t\)为边带项
频域表达式
\[ S_{AM}(w) = \pi A_0 [ \delta(w + w_c) + \delta (w - w_c)] + \frac{1}{2} [ M(w+w_c) + M(w - w_c) ] \]
其中\(\pi A_0 [ \delta(w + w_c) + \delta (w - w_c)]\)是载波项,\(\frac{1}{2} [ M(w+w_c) + M(w - w_c) ]\)是边带项
调制信号的频谱图
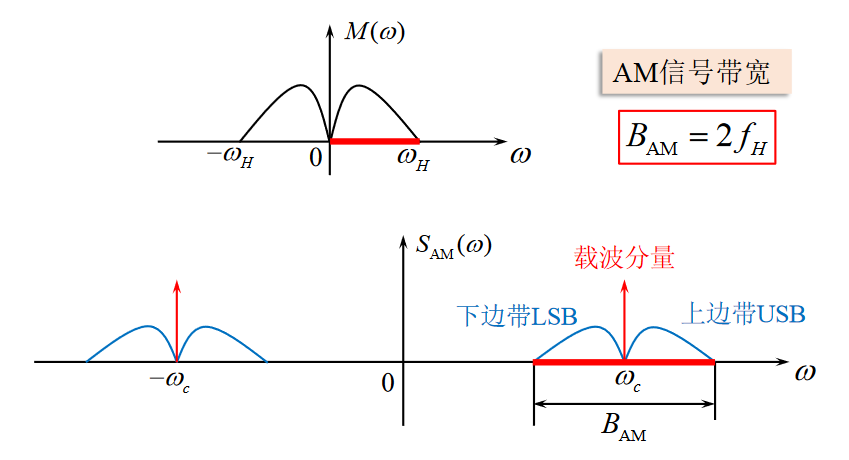
因为调制信号包含了上下两条正比于m(t)的边带(调制系数\(a\)小于等于1),所以频谱中的带宽是两倍的m(t)带宽。
AM信号在\(1\Omega\)电阻上的平均功率等于\(s_{AM}(t)\)的均方值 \[ P_{AM} = \overline{ s_{AM}^2 (t) } = \overline{ [A_0 + m(t)]^2 \cos^2 w_c t } = \overline{ A_0^2 \cos^2 w_c t } + \overline{ m^2(t) \cos^2 w_c t } + \overline{ 2A_0 m(t) \cos^2 w_c t } \]
因为\(m(t)\)的均值为0,所以\(\overline{ m(t) } = 0\)
\[ P_{AM} = \frac{ A_0^2 }{2} + \frac{ \overline{ m^2(t) } }{ 2 } = P_c + P_s \]
\(P_c\)为载波功率,\(P_s\)为边带功率
调制效率\(\eta_{AM}\) = 有用功率(用于传输信息的边带功率) / 信号总功率
\[ \eta_{AM} = \frac{ P_s }{ P_{AM} } \]
AM调制优缺点:
- 优点
- 系统结构简单,价格低廉
- 缺点
- 功率利用率比较低(调制信号为单音余弦信号,\(a = 1\)时“满调幅”,\(\eta_{AM}\)最大为\(1/3\))
包络检波
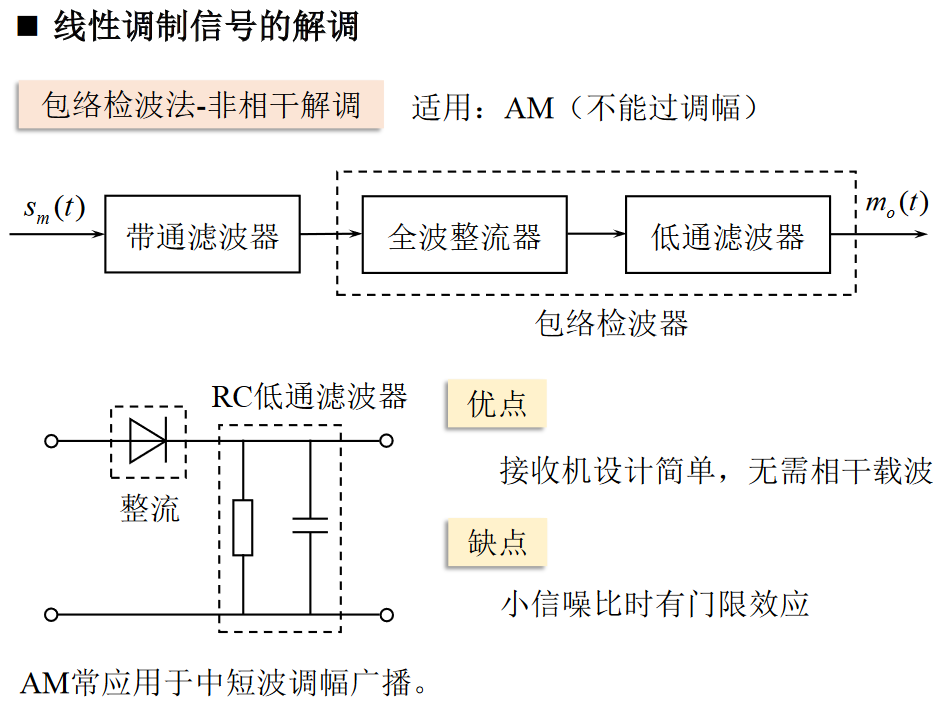
双边带调制
在AM调制模型中将\(A_0\)去掉,即可得到一种高调制效率的调制方式——抑制载波双边带信号(DSB-SC),简称双边带信号。 \[ s_{DSB}(t) = m(t) \cos w_c t \] 同样假设\(m(t)\)均值为0
DSB的频谱和AM频谱相近,只是没有了在\(\pm w_c\)处的\(\delta\)函数。 \[ S_{DSB}(w) = \frac{1}{2} [M(w + w_c) + M(w - w_c)] \]
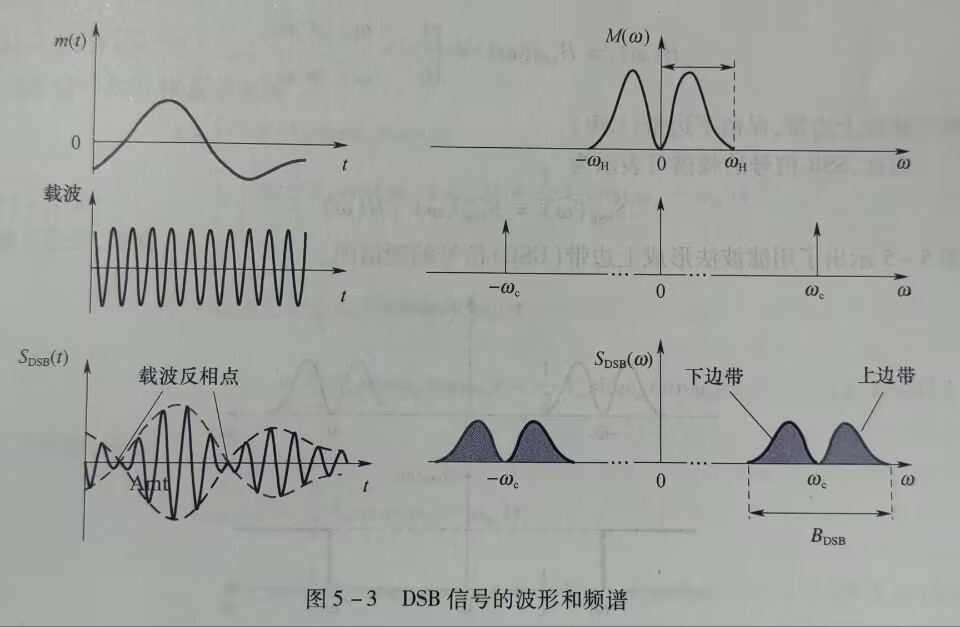
显然,DSB信号不存在载波分量,所以调制效率是100%。 但是DSB无法用包络检波恢复调制信号。解调方法是相干解调,也称同步检测。
DSB需要的传输带宽仍然是调制信号的两倍,即与AM信号带宽相同
单边带调制
注意到DSB信号的两个边带中任意一个都包含\(M(w)\)的所有频谱成分,因此只传输一个边带即可。这样能节省发送功率和1/2传输频带。
单边带调制(SSB)信号是将双边带信号中的一个边带滤掉而形成的。根据滤除方法,可以分为滤波法和相移法。
滤波法SSB信号
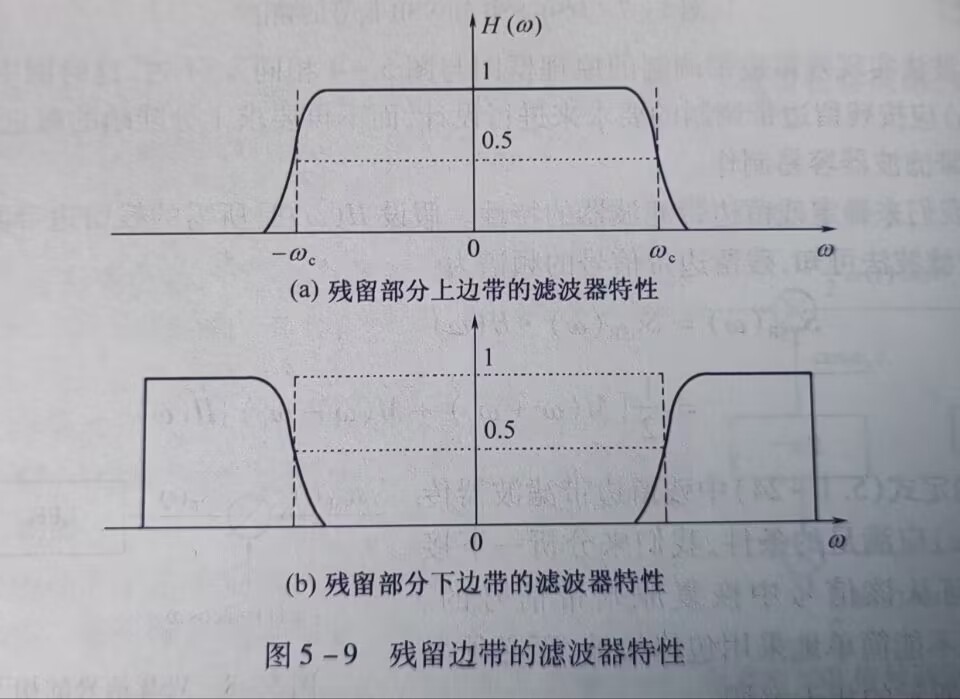
使用高通或低通滤波器\(H(w)\)得到SSB信号。高通对应上边带,低通对应下边带。 \[ S_{SSB}(w) = S_{DSB}(w) \cdot H(w) \] 如图
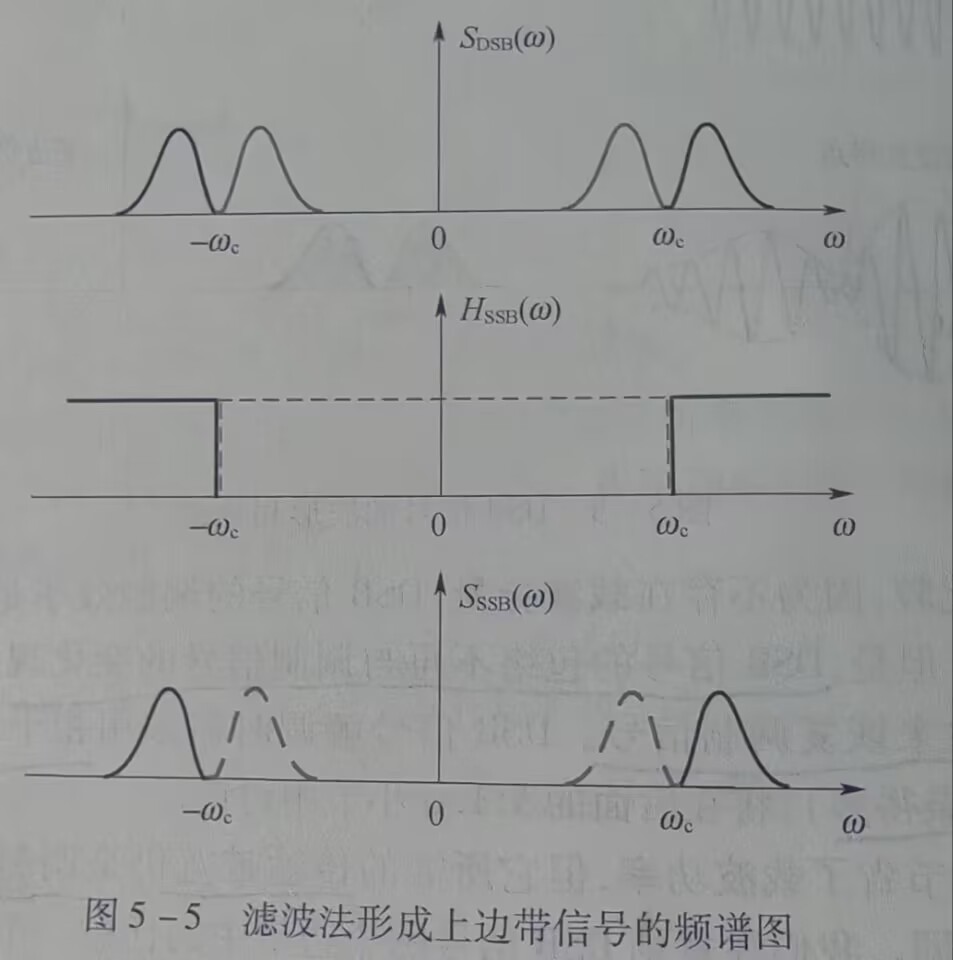
假如语音信号的最低频率为300Hz,则上下边带之间的频率间隔为600Hz,即允许过渡带为600Hz。实现滤波器的难易程度与过渡带相对载频的归一化值有关。值越小,边带滤波器就越难实现。
相移法SSB信号
需要借助希尔伯特变换描述SSB信号的时域表达式。
设单频调制信号 \[ m(t) = A_m\cos w_m t \] 载波为 \[ c(t) = \cos w_c t \] DSB信号的时域表达式 \[ \begin{aligned} s_{DSB}(t) &= A_m \cos w_m t \cos w_c t \\ &= \frac{1}{2} A_m\cos (w_c + w_m)t + \frac{1}{2} A_m\cos (w_c - w_m)t \end{aligned} \]
上边带是\(\frac{1}{2} A_m\cos (w_c + w_m)t = \frac{1}{2} A_m\cos w_m t\cos w_c t - \frac{1}{2} A_m \sin w_m t \sin w_c t\)
下边带是\(\frac{1}{2} A_m\cos (w_c - w_m)t = \frac{1}{2} A_m\cos w_m t\cos w_c t + \frac{1}{2} A_m \sin w_m t \sin w_c t\)
上下边带合并得到\(s_{SSB}(t)\) \[ s_{SSB}(t) = \frac{1}{2} A_m\cos w_m t\cos w_c t \mp \frac{1}{2} A_m \sin w_m t \sin w_c t \tag{1} \]
式中\(A_m \sin w_m t\)可以看成\(A_m\cos w_m t\)相移\(\frac{\pi}{2}\)的结果。把这一过程记为希尔伯特变换。
\[ A_m \hat{\cos} w_m t = A_m \sin w_m t \]
式(1)可以改写为 \[ s_{SSB}(t) = \frac{1}{2} A_m\cos w_m t\cos w_c t \mp \frac{1}{2} A_m \hat{\cos} w_m t \sin w_c t \]
推广到一般情况 \[ s_{SSB}(t) = \frac{1}{2} m(t) \cos w_c t \mp \frac{1}{2} \hat{m}(t) \sin w_c t \tag{2} \]
若\(m(t) <==> M(w)\),那么 \[ \hat{M}(w) = M(w) \cdot [-jsgnw] \tag{3} \] 符号函数 \[ sgnw = \left \{ \begin{aligned} 1 ~~~~ w>0 \\ -1 ~~~~ w<0 \end{aligned} \right. \tag{4} \]
系统框图
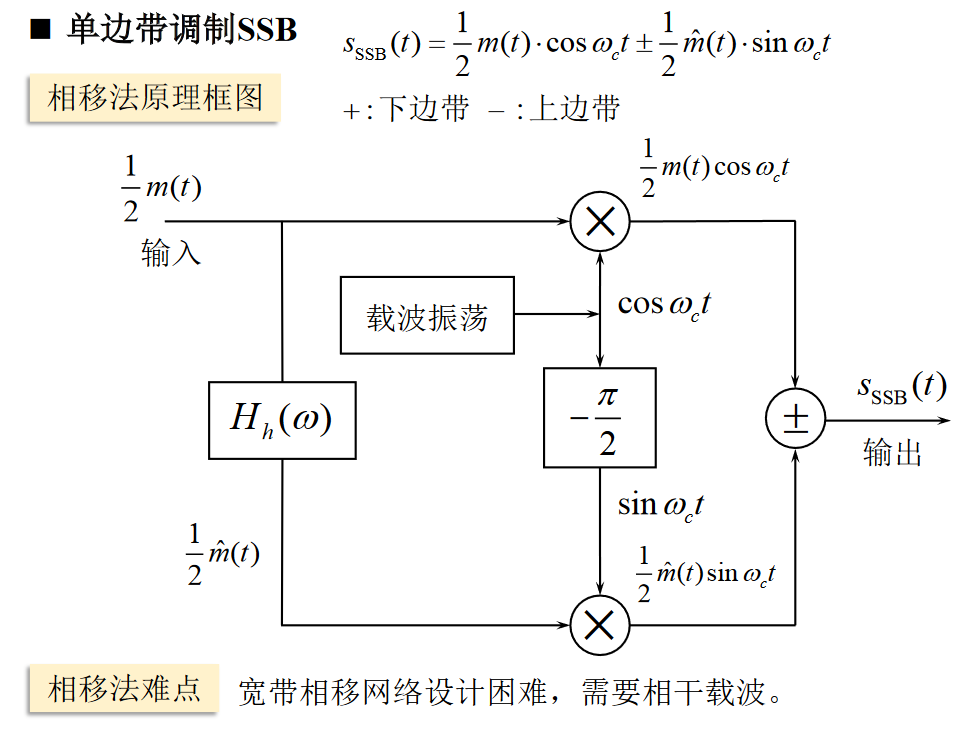
残留边带调制
VSB特点:不需要滤波器有十分陡峭的截止特性。
设\(H(w)\)是残留边带滤波器的传函。 \[ S_{VSB}(w) = S_{DSB}(w) \cdot H(w) = \frac{1}{2} [ M(w + w_c) + M(w - w_c) ] H(w) \]
残留边带相干解调
残留边带信号\(s_{VSB}(t)\)与相干载波\(2\cos w_c t\)的乘积为 \[ s_p(t) = 2s_{VSB}(t) \cos w_c t \] \(s_p(t)\)对应的频谱为 \[ \begin{aligned} S_p(w) &= [S_{VSB}(w + w_c) + S_{VSB}(w - w_c)] \\ &= \frac{1}{2} [ M(w + 2w_c) + M(w) ] H(w + w_c) + \frac{1}{2} [ M(w) + M(w - 2w_c) ] H(w - w_c) \end{aligned} \tag{5} \] 式中\(M(w - 2w_c),~M(w + 2w_c)\)是\(M(w)\)搬移到\(2w_c\)的频谱,可以用低通滤波器滤除。
滤波后得到 \[ S_d(w) = \frac{1}{2} M(w) [H(w + w_c) + H(w - w_c)] \]
为了无失真,\(H(w + w_c) + H(w - w_c)\)应该是一个常数。且\(|w| \leq w_H\),\(w_H\)是调制信号的截止频率(\(H(w)\)必须遵循的条件)。
VSB例题

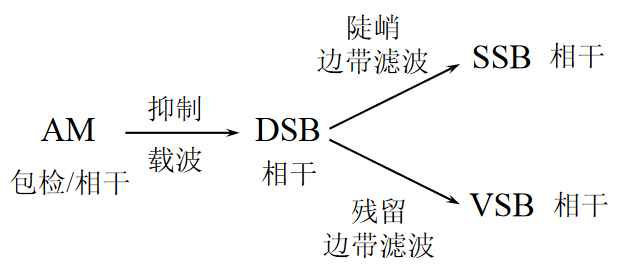
四类线性调制关系
线性调制matlab代码
AM调制代码
1 | |
角度调制
基本概念:载波的频率随调制信号变化称为调频(FM)。载波相位随调制信号变化称为调相(PM)。调制过程幅值不发生变化。统称角度调制。
特点:已调信号不再是原调制信号的频谱搬移,而是频谱的非线性变换。所以是非线性调制。
优势:较高的抗噪声性能 缺点:较大的带宽
FM,PM的一般表达式 \[ s_m(t) = A\cos [w_c t + \phi (t)] \tag{6} \]
\(A\)是载波的恒定振幅;\([w_c t + \phi (t)]\)是信号的瞬时相位,记为\(\theta(t)\);\(\phi(t)\)为相对于载波相位\(w_c t\)的瞬时相位偏移;\(d[w_c t + \phi (t)]/dt\)是信号的瞬时角频率,记为\(w(t)\);\(d\phi(t)/dt\)是相对于载频\(w_c\)的瞬时频偏。
PM:瞬时相位偏移随调制信号作线性变化 \[ \phi(t) = K_p m(t) \tag{7} \]
(7)带入(6) \[ s_{PM}(t) = A\cos [w_c t + K_p m(t)] \]
FM:瞬时频率偏移随调制信号作线性变化 \[ \frac{ d\phi(t) }{dt} = K_f m(t) \tag{8} \]
(8)带入(6) \[ s_{FM} = A\cos [w_c t + K_f \int m(\tau)d\tau] \]
如果预先不知道调制信号\(m(t)\)的具体形式,则无法判断已调信号是调相还是调频。
单频调制FM与PM
设调制信号为单一频率的正弦波 \[ m(t) = A_m\cos w_m t = A_m\cos 2\pi f_m t \] 对载波进行相位调制 \[ \begin{aligned} s_{PM}(t) &= A\cos [w_c t + K_p A_m \cos w_m t] &= A\cos [w_c t + m_p \cos w_m t] \end{aligned} \] \(m_p\)称为调相指数,表示最大的相位偏移
对载波进行频率调制 \[ \begin{aligned} s_{FM}(t) &= A\cos [w_c t + K_f A_m \int \cos w_m \tau d\tau] \\ &= A\cos [w_c t + m_f \sin w_m t] \end{aligned} \] \(m_f\)是调频指数 \[ m_f = \frac{ K_f A_m }{ w_m } = \Delta w / w_m = \Delta f / f_m \]
\(\Delta w\)是最大角频偏;\(\Delta f\)是最大频偏
波形
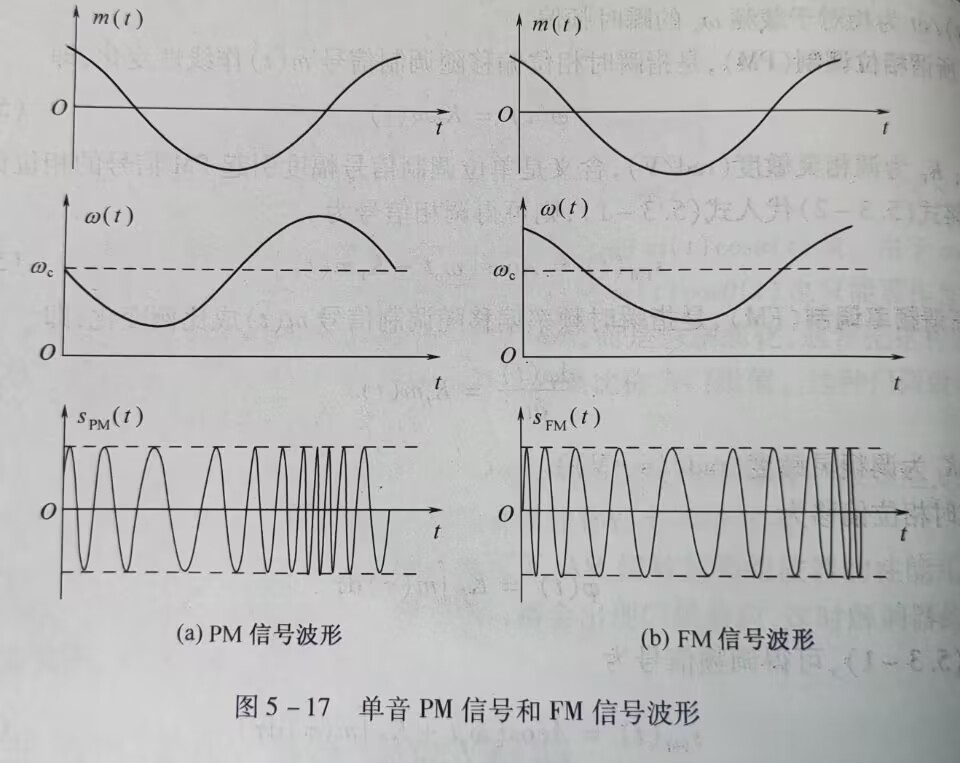
FM与PM之间的关系
FM和PM可以相互转换
窄带调频(NBFM)
FM信号最大瞬时相移满足 \[ \left| K_f \int m(\tau) d\tau \right| \ll \frac{\pi}{6} ~~~~ (或0.5) \tag{9} \]
FM信号一般表达式(6)展开得到 \[ \begin{aligned} s_{FM}(t) &= A\cos [w_c t + K_f \int m(\tau) d\tau] \\ &= A\cos w_c t \cos [ K_f \int m(\tau) d\tau ] - A\sin w_c t \sin [K_f \int m(\tau) d\tau] \end{aligned} \tag{10} \] 满足式(9)时,有 \[ \cos [ K_f \int m(\tau) d\tau ] \approx 1 \] \[ \sin [K_f \int m(\tau) d\tau] \approx K_f \int m(\tau) d\tau \]
所以(10)可以化简为 \[ s_{NBFM} (t) \approx A\cos w_c t - [ A K_f \int m(\tau) d\tau] \sin w_c t \] 其频域表达式 \[ S_{NBFM} (w) = \pi A [\delta(w + w_c) + \delta (w - w_c)] + \frac{AK_f}{2} \left[ \frac{M(w - w_c)}{w-w_c} - \frac{M(w+w_c)}{w+w_c}\right] \]
和AM的频谱比较, \[ S_{AM}(w) = \pi A[\delta(w + w_c) + \delta (w - w_c)] + \frac{1}{2} [M(w-w_c) + M(w+w_c)] \] 二者都含有一个载波和位于\(\pm w\)处的两个边带,所以他们的带宽相同,都是调制信号最高频率的两倍。不同的是,NBFM的两个边频分别乘了因式\(1/(w - w_c),~~ 1/(w + w_c)\) ,由于因式是频率的函数,所以这种加权是频率的加权,加权结果引起调制信号频谱失真。另外,NBFM的一个边带和AM反相。
宽带调频
不满足式(9)的时候,就是宽带调频
设调制信号为单一频率的正弦波 \[ m(t) = A_m\cos w_m t = A_m\cos 2\pi f_m t \] \[ s_{FM}(t) = A\cos [w_c t + m_f \sin w_m t] \] 将\(s_{FM}(t)\)展开 \[ s_{FM}(t) = A\cos w_c t \cdot \cos (m_f \sin w_m t) - A\sin w_c t \cdot \sin (m_f \sin w_m t) \tag{11} \] 将式中两个因子分别展开成如下傅里叶级数 \[ \begin{aligned} \cos (m_f \sin w_m t) = J_0(m_f) + \sum_{n=1}^{\infty} 2J_{2n}(m_f)\cos 2n w_m t \\ \sin (m_f \sin w_m t) = 2 \sum_{n=1}^{\infty} 2J_{2n-1}(m_f)\sin (2n-1) w_m t \end{aligned} \tag{12} \] \(J_{n}(m_f)\)为第一类n阶贝塞尔函数
将(12)带入(11),利用贝塞尔函数性质 \[ J_{-n}(m_f) = -J_{n}(m_f) ~~~~ n是奇数 \] \[ J_{-n}(m_f) = J_{n}(m_f) ~~~~ n是偶数 \]
得到FM信号傅里叶级数展开式为 \[ s_{FM}(t) = A\sum_{n=-\infty}^{\infty} J_n (m_f) \cos (w_c + nw_m) t \] 其频谱 \[ S_{FM}(w) = \pi A \sum_{n=-\infty}^{\infty} J_n (m_f) [\delta(w - w_c -nw_m) + \delta(w + w_c + nw_m)] \]
贝塞尔函数图像: 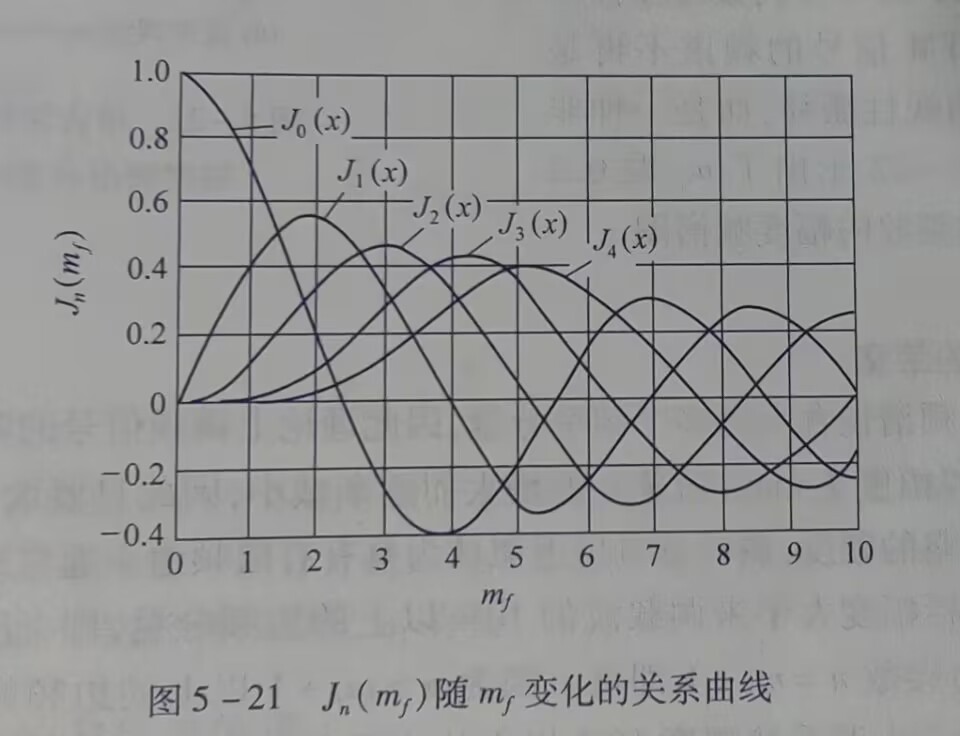
调频频谱图像: 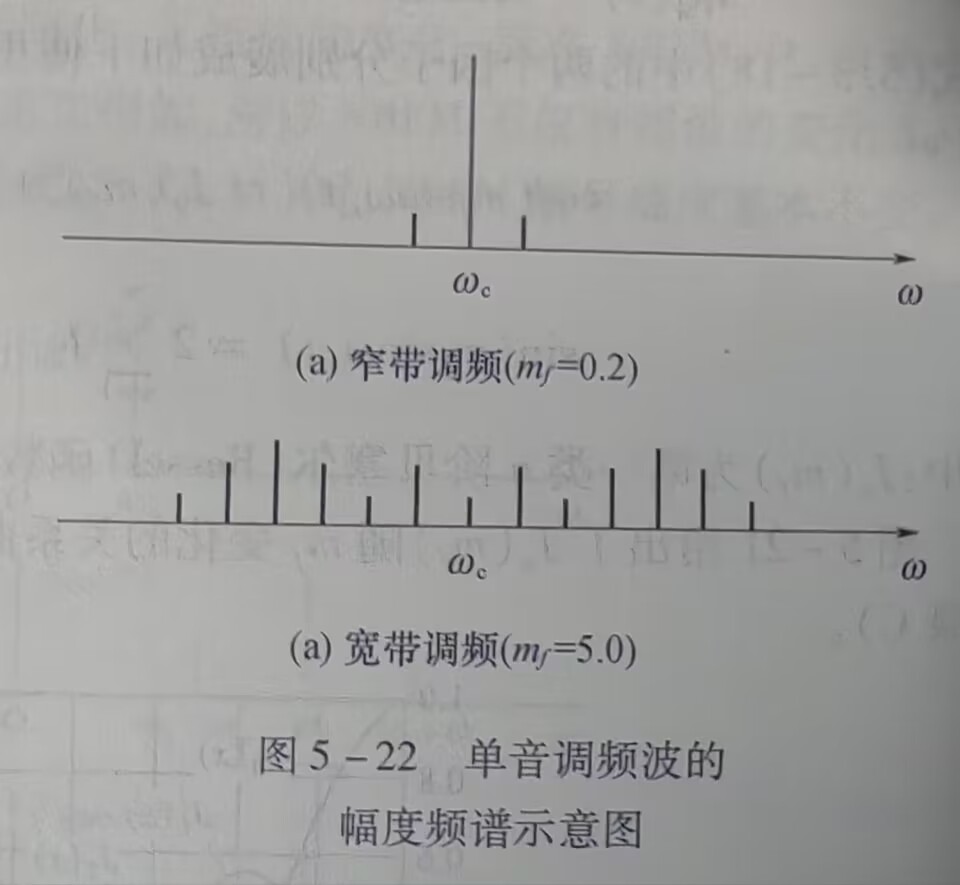
调频信号的带宽: 调频信号的频谱看似有无限多频率分量,理论上需要无限大带宽。实际上\(J_n (m_f)\)随着\(n\)的增大而逐渐减小。因此只要取适当的n值使边频分量小到可以忽略的程度,调频信号可近似认为具有有限频谱。通常采用的原则是:信号的频带宽度应包括幅度大于未载波的10%以上的边频分量,即\(|J_n (m_f)|\geq 0.1\)。当\(m_f \geq 1\)以后,取边频数\(n=m_f+1\)即可。
调频波的有效带宽为: \[ B_{FM} = 2(m_f + 1)f_m = 2(\Delta f + f_m) \tag{13} \] 式(13)就是计算调频带宽的卡森(Carson)公式
当\(m_j \ll 1\)时 \[ B_{FM} \approx 2f_m ~~~~ (NBFM) \]
当\(m_j \gg 1\)时 \[ B_{FM} \approx 2\Delta f ~~~~ (WBFM) \]
当信号不是单一频率时候: \[ B_{FM} = 2(m_f + 1)f_m = 2(\Delta f + f_m) \] \(f_m\)是调制信号的最高频率,\(m_f\)是调制信号的最大频偏。
调频信号功率分配
调频信号\(s_{FM}(t)\)在\(1\Omega\)电阻上消耗的平均功率为: \[ P_{FM} = \overline{s_{FM}^{2} (t)} \] 利用帕塞瓦尔定理 \[ P_{FM} = \overline{s_{FM}^{2} (t)} =\frac{A^2}{2} \sum_{n=-\infty}^{\infty} J_n^2 (m_f) \] 贝塞尔函数性质: \[ \sum_{n=-\infty}^{\infty} J_n^2 (m_f) = 1 \] 因此 \[ P_{FM} = \frac{A^2}{2} = P_c \] \(P_c\)是未调载波的平均功率。调制后总功率不变,只是将原来的功率中的一部分分配给每个边频分量。 调制的过程只是进行功率的重新分配,分配的原则与调频指数\(m_f\)有关。
调频信号产生与解调
直接调频法
压控振荡器:可以由外部电压控制振荡频率的振荡器(VCO)。
每个压控振荡器自身就是FM调制器,因为振荡频率正比于输入控制电压 \[ w_i(t) = w_0 + K_f m(t) \]
优缺点: - 优点:线性调频,频偏较大。 - 缺点:频率稳定度不高
运用锁相环(PLL)调制器可以提高频率稳定度,但是低频调制特性差。
间接调频法
先将调制信号积分,然后对载波进行调相,即可产生一个NBFM信号,再经过n次倍频器得到
优缺点: - 优点:频率稳定度好 - 缺点:需要多次倍频混频,电路复杂
获得NBFM:
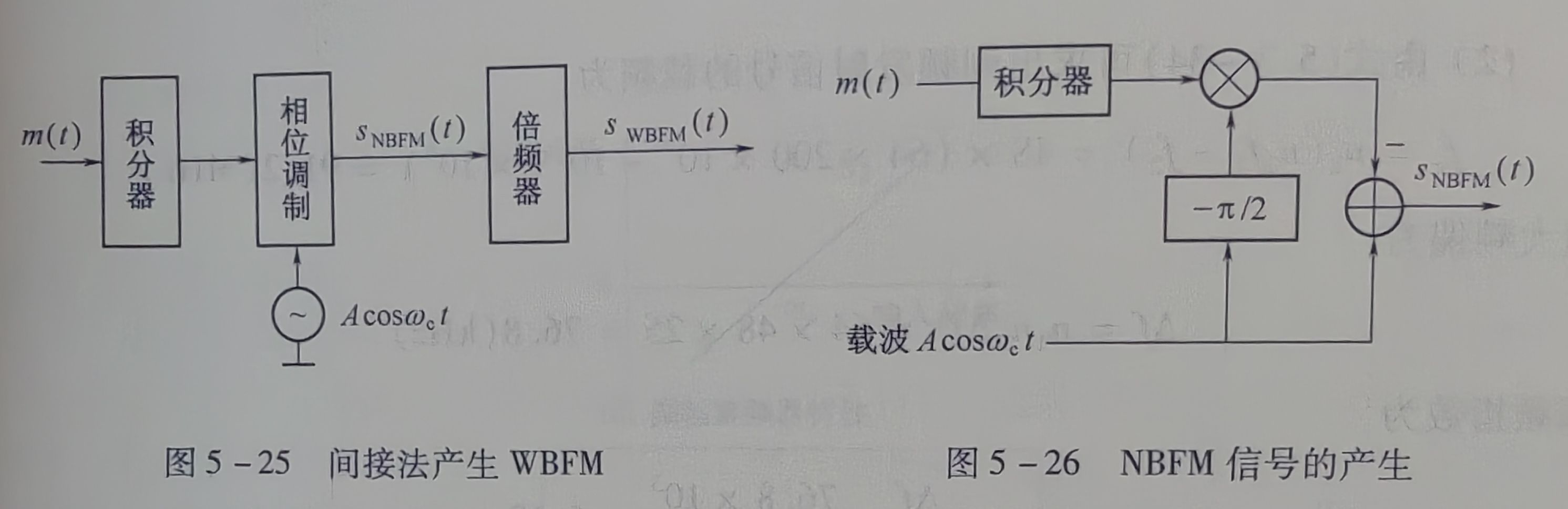
\[ s_{NBFM} (t) \approx A\cos w_c t - [ A K_f \int m(\tau) d\tau] \sin w_c t \]
要将NBFM信号倍频得到WBFM信号,需要倍频器。
理想平方律器件: \[ s_o(t) = as_i^2(t) \]
当\(s_i(t) = A\cos[w_c t + \phi(t)]\)
\[ s_o(t) = \frac{1}{2} aA^2 \left\{ 1 + \cos[ 2w_c t + 2\phi(t) ] \right\} \]
可以看到载波频率和调频指数都变为原来的两倍。
来道例题~~

调频信号解调
相干解调仅适用于NBFM信号。非相干解调对NBFM、WBFM均适用。
调频信号一般表达式 \[ s_{FM}(t) = A\cos [w_c t + K_f \int m(\tau) d\tau] \] 解调器输出 \[ m_o(t) \propto K_f m(t) \]
非相干解调
解调需要产生一个与输入调频信号的频率呈线性关系的输出电压。完成这种频率——电压转换关系的器件是频率检波器,简称鉴频器。
鉴频器 = 微分器 + 包络检波器
调频信号\(s_{FM}(t)\)经过微分器输出为 \[ s_d(t) = -A[ w_c + K_f m(t) ] \sin \left[ w_c t + K_f \int m(\tau) d\tau \right] \]
包络检波器将幅度变化检出并滤去直流,低通滤波后输出 \[ m_o(t) = K_d K_f m(t) \] \(K_d\)为鉴频器灵敏度。
相干解调
窄带调频信号 \[ s_{NBFM} (t) \approx A\cos w_c t - [ A K_f \int m(\tau) d\tau] \sin w_c t \]
相干载波 \[ c(t) = -\sin w_c t \]
二者相乘 \[ s_p(t) = - \frac{A}{2} \sin 2w_c t + \frac{A}{2} \left[ K_f \int m(\tau)]d\tau \right] \cdot (1 - \cos 2w_c t) \]
低通滤波 \[ s_d (t) = \frac{A}{2} K_f \int m(\tau)]d\tau \]
经过微分器处理 \[ m_o(t) = \frac{ AK_f }{ 2 } m(t) \]
抗噪声性能
信道中加性高斯白噪声是普遍存在的噪声。加性噪声被认为只对已调信号的接收产生影响。通信系统的抗噪声性能可以用解调器的抗噪声性能衡量

一般认为图中\(n_i(t)\)是平稳窄带高斯噪声 \[ n_i(t) = n_c(t) \cos w_0 t - n_s(t) \sin w_0 t \] \(w_0\)是带通滤波器的中心频率
\[ \overline{ n_i^2(t) } = \overline{ n_c^2(t) } = \overline{ n_s^2(t) } = N_i = n_0 B \] \(n_0\)是白噪声功率谱密度,\(B\)是带通滤波器带宽也是已调信号频带宽度。
信噪比 \[ \frac{S_o}{N_o} = \frac{ 解调器输出有用信号的平均功率 }{ 解调器输出噪声的平均功率 } = \frac{ \overline{m_o^2(t)} }{ n_o^2(t) } \]
为了便于比较同类调制系统采用不同解调器时的性能,引入输出信噪比和输入信噪比的比值——调制制度增益或信噪比增益\(G\) \[ G = \frac{ S_o/N_o }{ S_i / N_i } \] \(G\)的大小反应调制制度的优劣。
\[ \frac{S_i}{N_i} = \frac{ 解调器输入已调信号的平均功率 }{ 解调器输入噪声的平均功率 } = \frac{ \overline{s_m^2(t)} }{ n_i^2(t) } \]
线性系统抗噪声性能
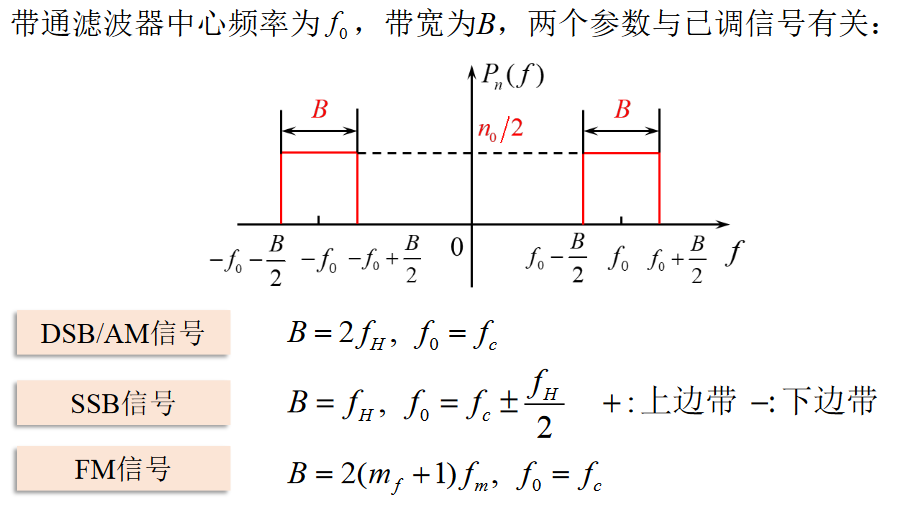
DSB系统噪声

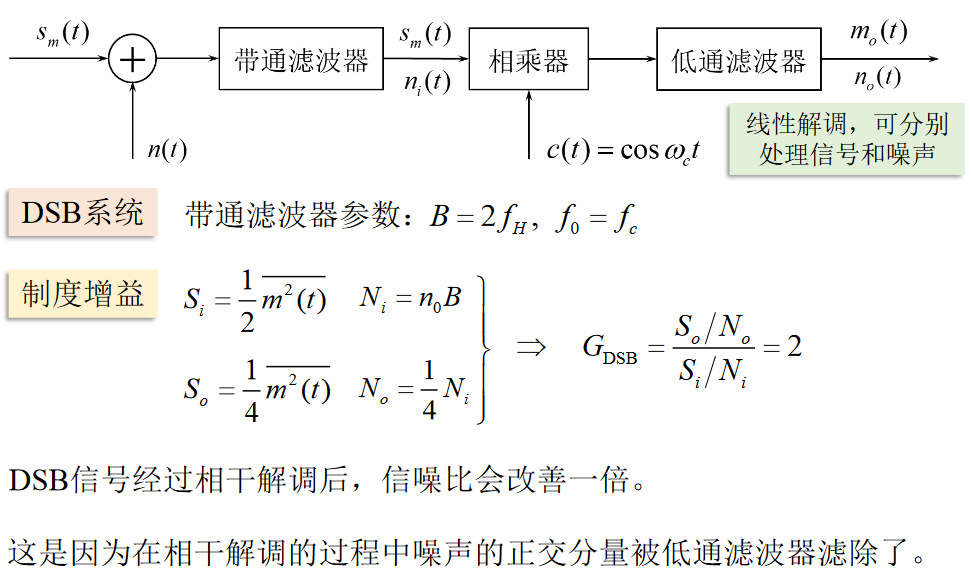
SSB系统噪声

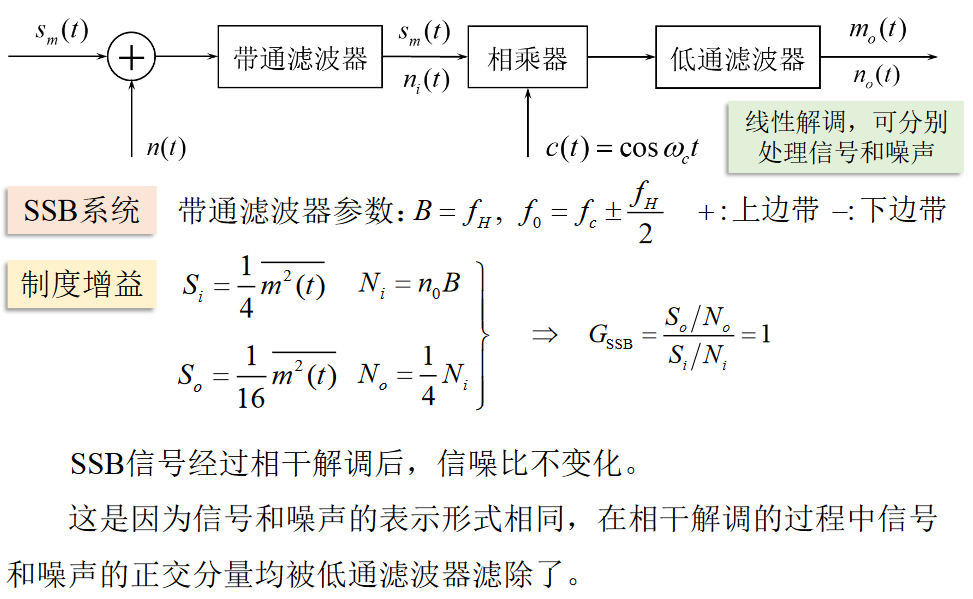
DSB,SSB抗噪声性能比较
输入功率\(S_i\),功率谱密度\(n_0\),基带信号最高频率\(f_H\)都相同时
DSB带宽\(B=2f_H\),SSB带宽\(B=f_H\)
\[ \left( \frac{S_o}{N_o} \right)_{DSB} = 2 \frac{S_i}{N_i} = \frac{S_i}{n_0 f_H} \]
\[ \left( \frac{S_o}{N_o} \right)_{SSB} = \frac{S_i}{N_i} = \frac{S_i}{n_0 f_H} \]
DSB,SSB抗噪声性能相同
AM系统噪声
输入信号 \[ s_m(t) = [A_0 + m(t)] \cos w_ct \] 噪声 \[ n_i(t) = n_c(t)\cos w_c t - n_s(t) \sin w_c t \]
\[ S_i = \overline{ s_m^2(t) } = \frac{A_0}{2} + \frac{ \overline{ m^2(t) } }{2} \] \[ N_i = \overline{ n_i^2(t) } = n_0 B \]
\[ \frac{S_i}{N_i} = \frac{ A_0^2 + \overline{ m^2(t) } }{ 2n_0 B } \]
解调器输入的时混合波形 \[ s_m (t) + n_i (t) = E(t) \cos [ w_c t + \Phi(t) ] \] \[ E(t) = \sqrt{ [ A_0 + m(t) + n_c(t) ]^2 + n_s^2(t)} \] \[ \Phi(t) = \arctan \left[ \frac{n_s(t)}{ A_0 + m(t) + n_c(t) } \right] \]
显然\(E(t)\)是所求包络。
大信噪比情况:
\[ [A_0 + m(t)] \gg \sqrt{ n_c^2(t) + n_s^2(t) } \] \(E(t)\)可以化简为 \[ E(t) = A_0 + m(t) + n_c(t) \]
- 注:利用近似公式\((1 + x)^{1/2} \approx 1 + x/2\)
输出信号功率为 \[ S_o = \overline{ m^2(t) } \] 输出噪声功率 \[ N_o = \overline{ n_c^2(t) } = \overline{ n_i^2(t) } = n_0B \] 输出信噪比 \[ \frac{S_o}{N_o} = \frac{ \overline{ m^2(t) } }{ n_0B } \]
调制制度增益 \[ G = \frac{ 2\overline{ m^2(t) } }{ A_0^2 + \overline{ m^2(t) } } \] \(G\)最大为\(2/3\)
小信噪比情况
\[ E(t) = R(t) \sqrt{ 1 + \frac{ 2[A_0 + m(t)] }{ R(t) } \cos \theta(t) } \] 其中 \[ \begin{aligned} R(t) = \sqrt{ n_c^2(t) + n_s^2(t) } \\ \theta(t) = \arctan \left[ \frac{ n_s(t) }{ n_c(t) } \right] \\ \cos \theta (t) = \frac{ n_c(t) }{R(t)} \end{aligned} \]
再次利用近似公式\((1 + x)^{1/2} \approx 1 + x/2\)
\[ E(t) = R(t) + [A_0 + m(t)]\cos \theta(t) \]
非线性系统抗噪声性能

性能比较
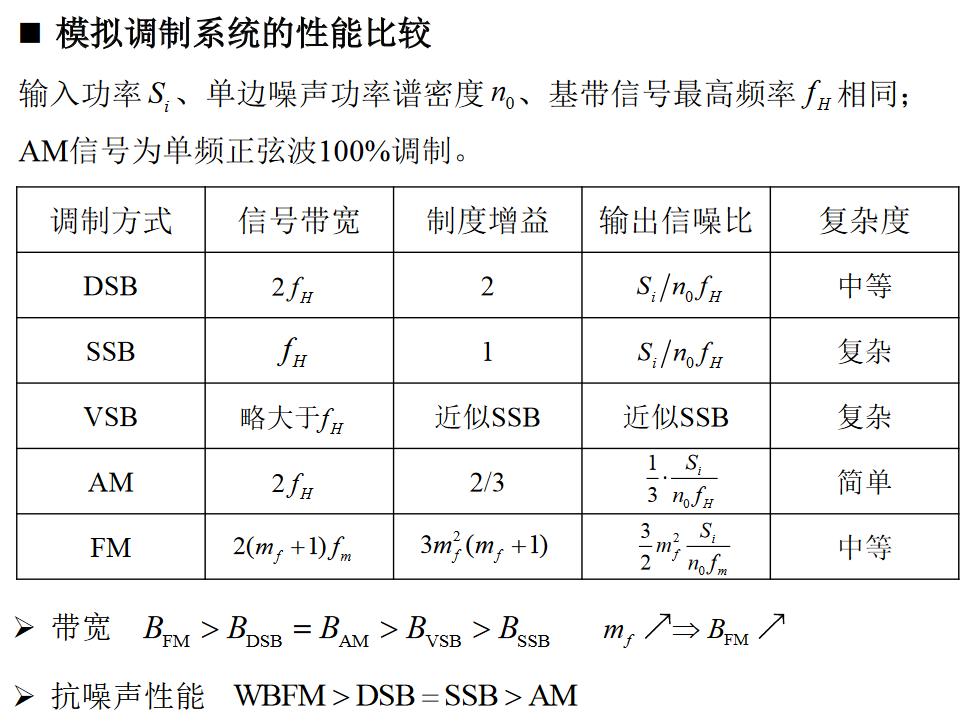
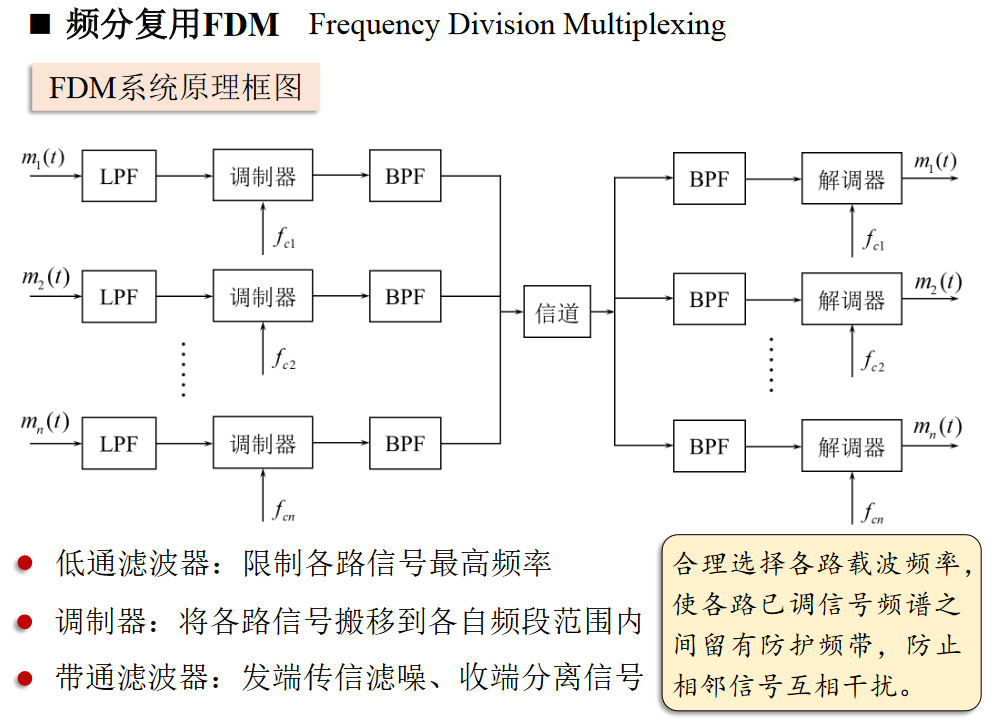
频分复用FDM