Truthtable1

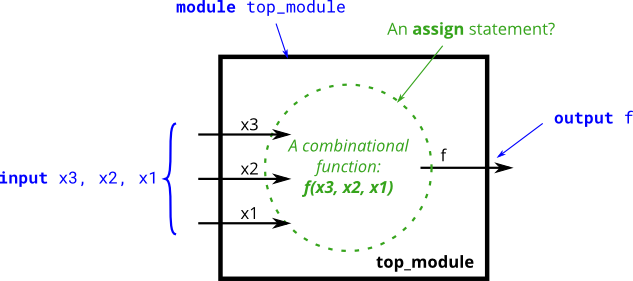
In the previous exercises, we used simple logic gates and combinations of several logic gates. These circuits are examples of combinational circuits. Combinational means the outputs of the circuit is a function (in the mathematics sense) of only its inputs. This means that for any given input value, there is only one possible output value. Thus, one way to describe the behaviour of a combinational function is to explicitly list what the output should be for every possible value of the inputs. This is a truth table.

For a boolean function of N inputs, there are \(2^N\) possible input combinations. Each row of the truth table lists one input combination, so there are always \(2^N\) rows. The output column shows what the output should be for each input value.

row	inputs	outputs
number	x3 x2 x1	f
0	0 0 0	0
1	0 0 1	0
2	0 1 0	1
3	0 1 1	1
4	1 0 0	0
5	1 0 1	1
6	1 1 0	0
7	1 1 1	1

The above truth table is for a three-input, one-output function. It has 8 rows for each of the 8 possible input combinations, and one output column. There are four inputs combinations where the output is 1, and four where the output is 0.

A Bit of Practice

Create a combinational circuit that implements the above truth table.

Truthtable1

solution

module top_module( 
    input x3,
    input x2,
    input x1,  // three inputs
    output f   // one output
);
	assign f = ~x3 & x2 | x3 & x1;
endmodule